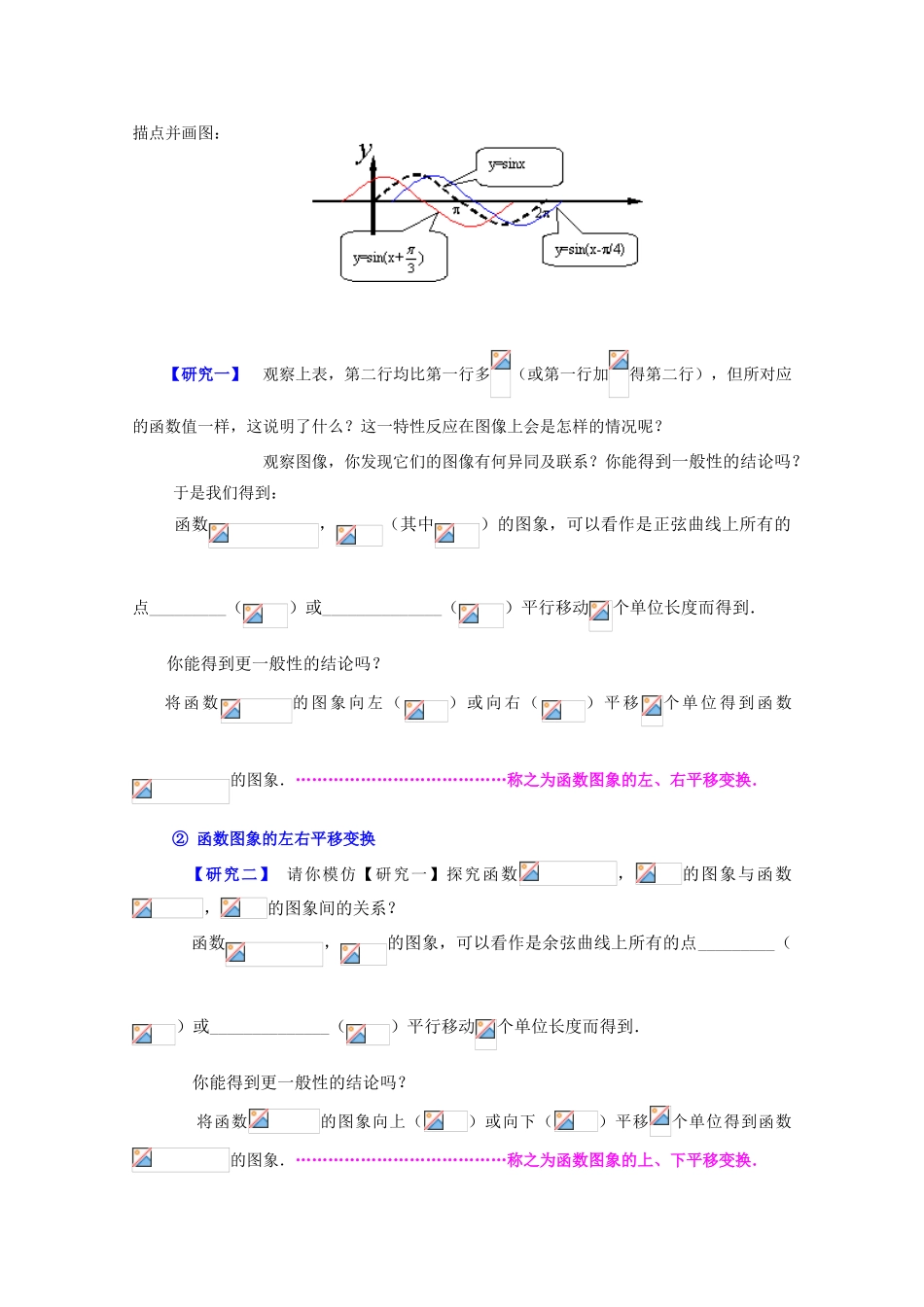
1.5 函数的图象一、导学目标 1.会用“五点法”作出函数以及函数的图象; 2.理解、、对函数的图象的影响;3.能够将的图象变换到的图象.4.理解振幅、周期、频率、初相的定义;5.会根据条件求解析式.二、尝试练习(一)探索与发现探究一、 平移变换① 函数图象的左右平移变换【案例 1】 画出函数 y=sinx,xR、y=sin(x+),x∈R、y=sin(x-),x∈R的简图【解】列表:x-x+02sin(x+)010–10xx-02sin(x–)010–10描点并画图:【研究一】 观察上表,第二行均比第一行多(或第一行加得第二行),但所对应的函数值一样,这说明了什么?这一特性反应在图像上会是怎样的情况呢? 观察图像,你发现它们的图像有何异同及联系?你能得到一般性的结论吗? 于是我们得到:函数,(其中)的图象,可以看作是正弦曲线上所有的点_________()或______________()平行移动个单位长度而得到.你能得到更一般性的结论吗?将函数的图象向左()或向右()平移个单位 得到 函数的图象.…………………………………称之为函数图象的左、右平移变换.② 函数图象的左右平移变换【研究二】 请你模仿【研究一】探究函数,的图象与函数,的图象间的关系?函数,的图象,可以看作是余弦曲线上所有的点_________()或______________()平行移动个单位长度而得到.你能得到更一般性的结论吗?将函数的图象向上()或向下()平移个单位得到函数的图象.…………………………………称之为函数图象的上、下平移变换.探究二、 伸缩变换① 函数图象的横向伸缩变换【案例3】画出函数 y=sin2x,xR;y=sinx,xR 的图象.【解】函数 y=sin2x,x∈R 的周期 T=. 我们先画在[0,π]上的简图,在[0, ]上作图,列表:描点并画图:【研究三】 观察上表,第一行的值应乘以得到第二行相应的值,但所对应的函数值一样,这说明了什么?这一特性反应在图像上会是怎样的情况呢? 观察图像,你发现的图像与的图像有何异同及联系?你能得到一般性的结论吗?试猜想函数的图像与的图像之间的关系,并将这一结论进行推广.于是我们得到:函数(其中且)的图象,可以看作是把正弦曲线上所有点的横坐标______________()或______________()到原来的2x02x0y=sin2x010-10倍(纵坐标不变)而得到.你能得到更一般性的结论吗?将函数的图象上所有点的横坐标缩短()或伸长()到原来的倍(纵坐标不变)得到函数()的图象.…………………………………这种变...