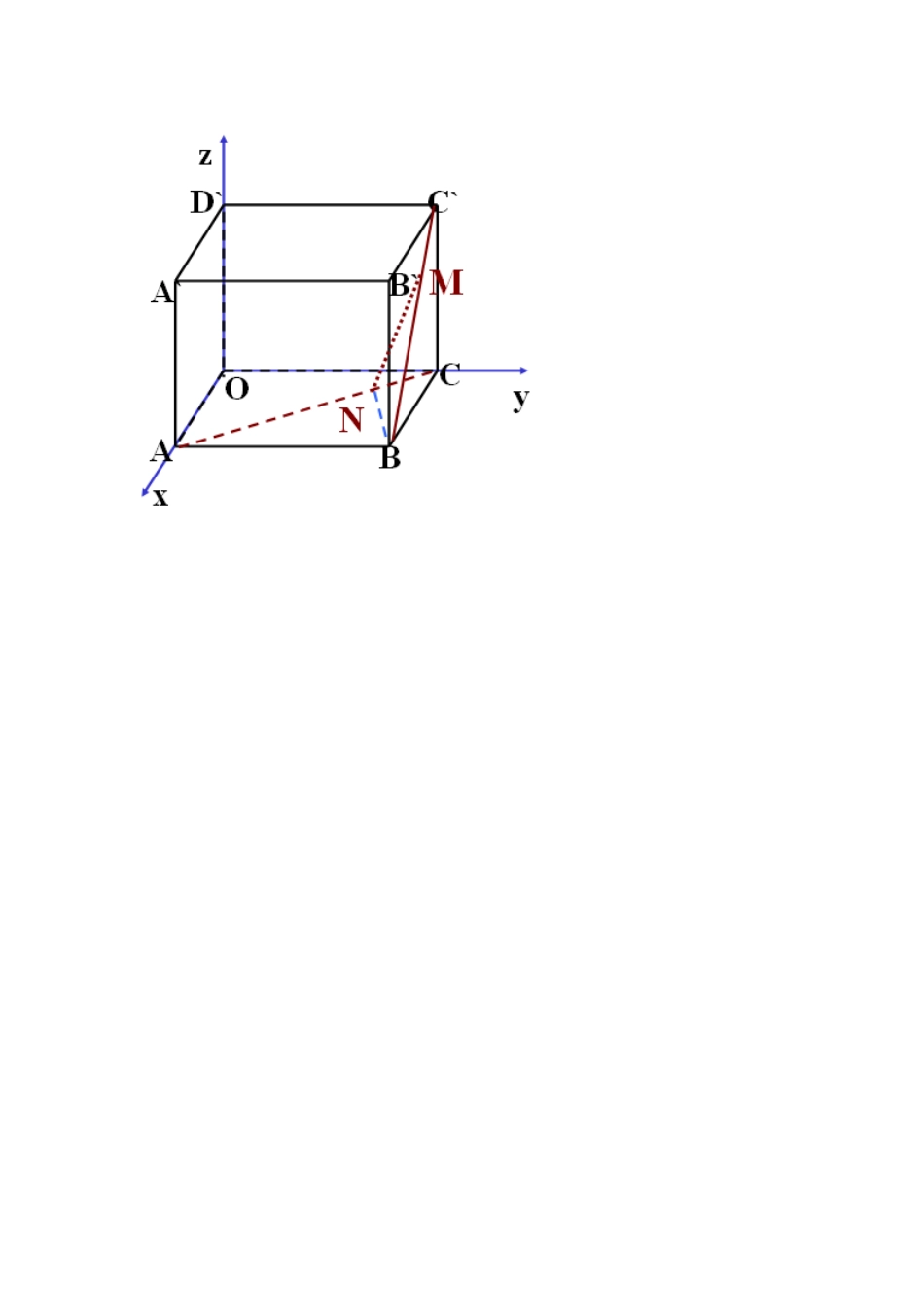
高中数学高一年级必修二第四章 第 4.3.2 节:空间中两点间的距离公式导学案A.学习目标通过特殊到一般的情况推导出空间两点间的距离公式B.学习重点、难点 重点:空间两点间的距离公式难点:一般情况下,空间两点间的距离公式的推导。C.学法指导通过运用空间直角坐标系的知识解决实际问题的学习,从而激发学生学习数学的 热情和兴趣。D.知识链接与距离有关的一些实物,同时距离公式的应用E.自主学习教师提出问题:提出学生在生活中对距离的认识,引导学生回忆,举例和相互交流。教师对学生的活动及时给予评价。F.合作探究1.引导学生思考、交流、讨论,对空间中两点间的距离进行讨论2.推导出空间两点间的距离公式G.课堂小结由学生整理学习了哪些内容?有什么收获?H.达标检测1、在空间直角坐标系中,任意两点 P1(x1,y1,z1)和 P2(x2,y2,z2)间的距离2 在空间直角坐标系中,已知两点 A、B 坐标,求出它们之间的距离:(1) A(2,3,5) B(3,1,4) ;(2)A(6,0,1) B(3,5,7)3 在 z 轴上求一点 M,使得点 M 到点 A(1,0,2)与点 B(1,-3,1)的距离相等。4 如图,正方体 OABC-D`A`B`C`的棱长为 a,|AN|=2|CN|,|BM|=2|MC`|,求 MN 的长.