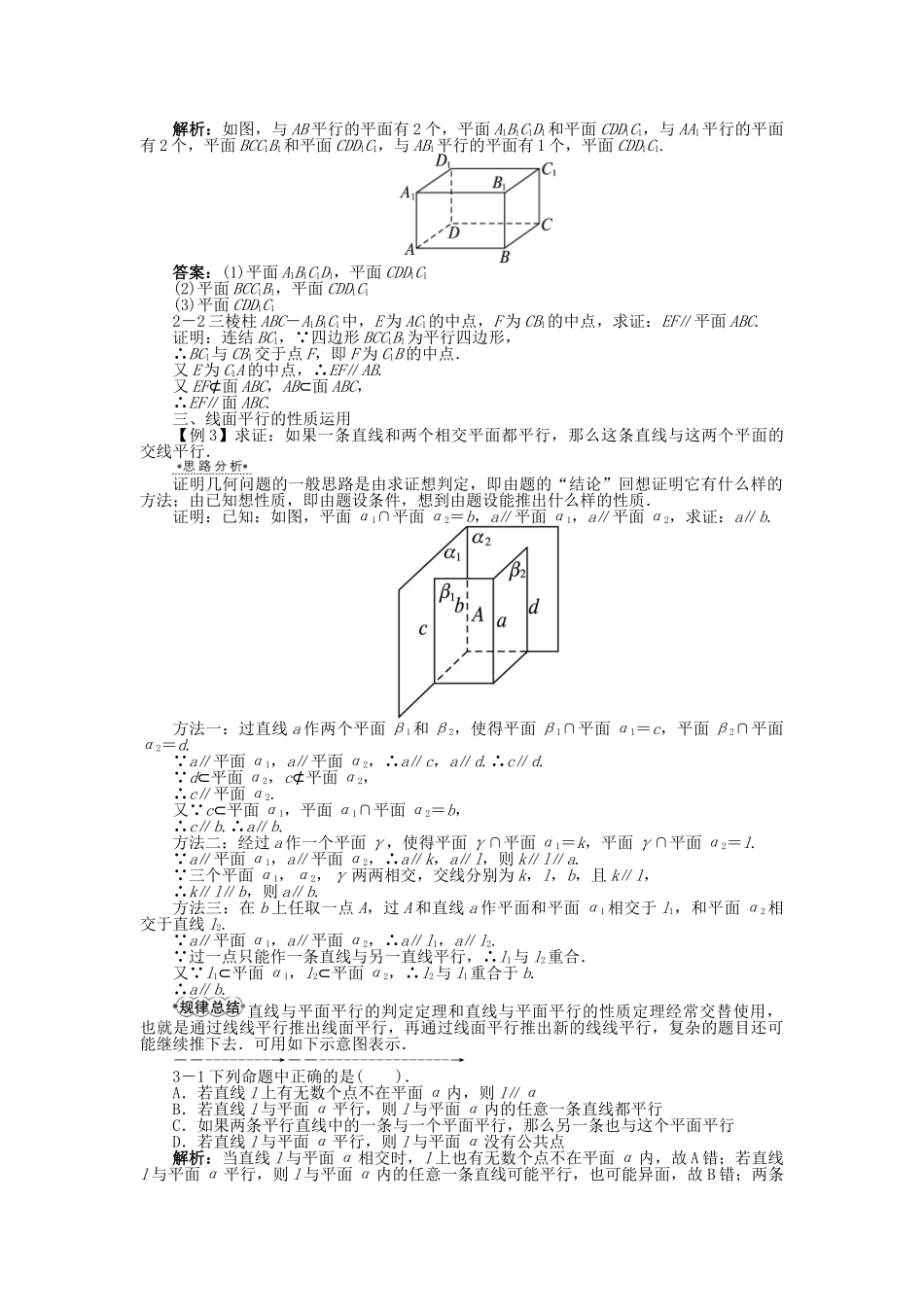
6.2.2 平行关系(1)1.直线 l 与平面 α 平行,记作 l∥α,是指直线 l 与平面 α 没有公共点.也就是说:l 与 α 的交集是空集.2.定理 2:一条直线与一个平面平行,则过该直线的任一平面与此平面的交线与该直线平行.这个定理称为直线与平面平行的性质定理.3.定理 3:平面外一条直线与此平面内的一条直线平行,则该直线与该平面平行.利用这个定理,可以由“线线平行”判定“线面平行”.我们称它为直线与平面平行的判定定理.4.空间四边形的定义:(1)命题“a∥b,a∥α,则 b∥α”是真命题吗?提示:假命题,有可能 b⊂α.(2)若直线 l 平行于平面 α 内的无数条直线,则直线 l 平行于平面 α 吗?提示:不一定.因为当直线 l 在平面 α 内时,与 l 平行的直线也有无数条.一、线线平行问题【例 1】已知正方体 ABCD-A1B1C1D1,E,F 分别为 AA1,CC1的中点,求证:BFED1.解答本题可先画出图形,再根据中点作辅助线,将立体图形问题转化为平面几何问题求解.证明:如图所示,取 BB1的中点 G,连结 GC1,GE, F 为 CC1的中点,∴BGC1F.∴四边形 BGC1F 为平行四边形.∴BFGC1.又 EGA1B1,A1B1C1D1,∴EGD1C1.∴四边形 EGC1D1是平行四边形.∴ED1GC1.∴BFED1.1-1 以下说法正确的个数是( ).① 没有公共点的两条直线平行;② 与同一条直线垂直的两条直线平行;③ 平行于同一条直线的两条直线平行;④ 相等的角,若一组对应边平行,则另一组对应边也平行.A.0 B.1 C.2 D.3解析:没有公共点的两条直线平行或异面,故①不正确;与同一条直线垂直的两条直线相交、平行或异面,故②错;根据平行直线的传递性可知③是正确的;对④,另一组对应边可能平行也可能不平行,故④不正确.答案:B1-2 如图所示,一平面与空间四边形 ABCD 的对角线 AC、BD 都平行,且交空间四边形的边 AB,BC,CD,DA 分别于 E,F,G,H,求证:四边形 EFGH 为平行四边形.证明: AC∥平面 EFGH,AC⊂平面 ACD,平面 ACD∩平面 EFGH=GH,∴AC∥GH.同理可证:AC∥EF,BD∥EH,BD∥FG.∴EF∥GH,EH∥FG,∴四边形 EFGH 为平行四边形.二、线面平行的判定【例 2】已知空间四边形 ABCD,P,Q 分别是△ABC 和△BCD 的重心,求证:PQ∥平面ACD.欲证线面平行,需证线线平行,即要证明 PQ 与平面 ACD 中的某条直线平行,根据条件,此直线为 AD.证明:如图,取 BC 的中点 E. P 是△ABC 的...