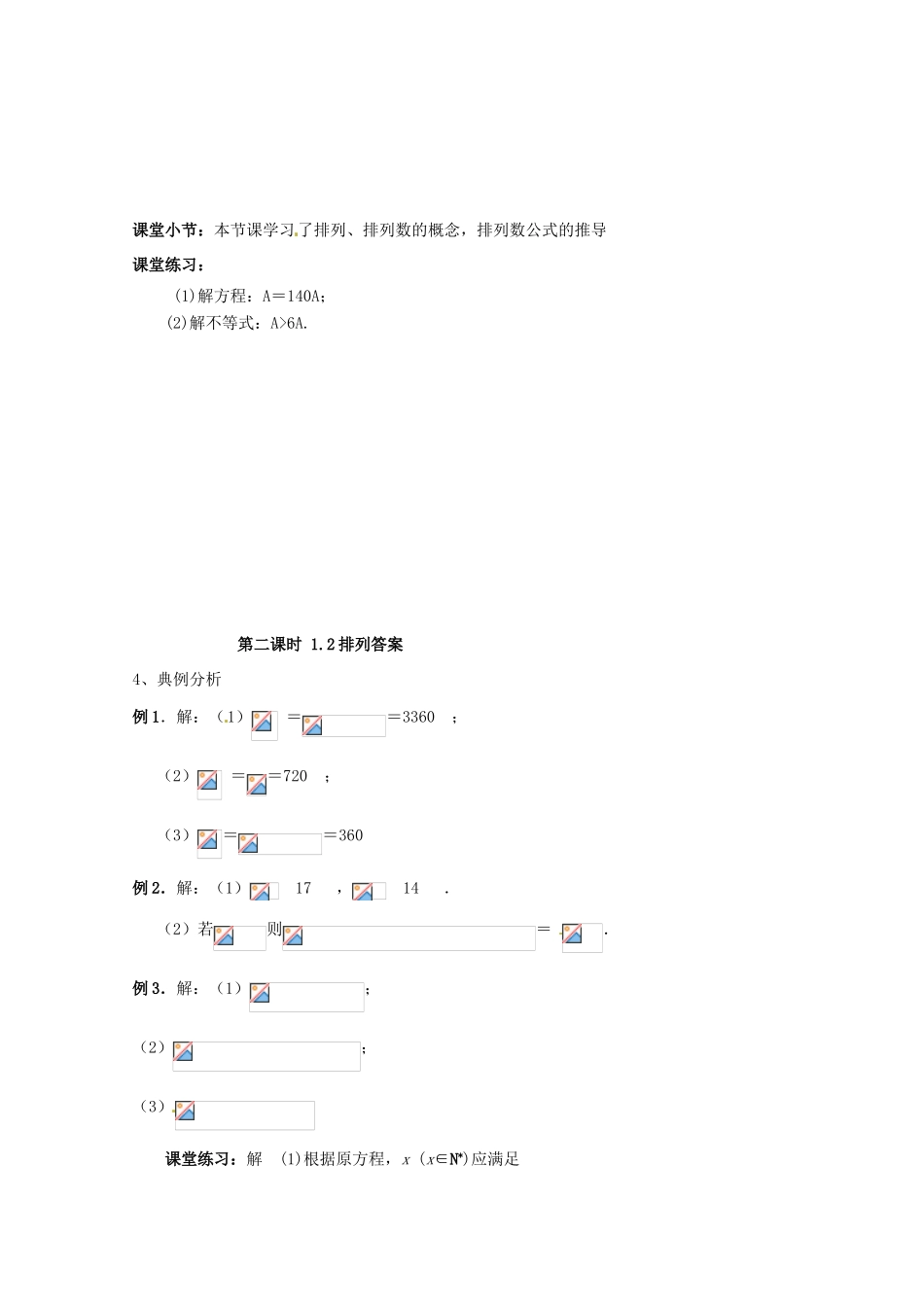
第二课时 1.2.1 排列学习目标:理解排列、排列数的概念,了解排列数公式的推导学习重点:理解排列、排列数的概念,了解排列数公式的推导学习过程:一、复习引入:1.分类计数原理:(1)加法原理:如果完成一件工作有k 种途径,由第 1 种途径有 n1种方法可以完成,由第 2 种途径有 n2种方法可以完成,……由第 k 种途径有 nk种方法可以完成。那么,完成这件工作共有 n1+n2+……+nk种不同的方法。2,乘法原理:如果完成一件工作可分为 K 个步骤,完成第 1 步有 n1种不同的方法,完成第 2 步有 n2种不同的方法,……,完成第 K 步有 nK 种不同的方法。那么,完成这件工作共有n1×n2×……×nk种不同方法二、学习新课:1.排列的概念:从个不同元素中,任取()个元素(这里的被取元素各不相同)按照一定的顺序排成一列,叫做从个不同元素中取出个元素的一个排列说明:(1)排列的定义包括两个方面:①取出元素,②按一定的顺序排列; (2)两个排列相同的条件:①元素完全相同,②元素的排列顺序也相同2.排列数的定义:从个不同元素中,任取()个元素的所有排列的个数叫做从个元素中取出元素的排列数,用符号表示注意区别排列和排列数的不同:“一 个排列”是指:从个不同元素中,任取个元素按照一定的顺序排成一列,不是数;“排列数”是指从个不同元素中,任取()个元素的所有排列的个数,是一个数所以符号只表示排列数,而不表示具体的排列3.排列数公式及其推导:求以按依次填个空位来考虑,排列数公式:=()说明:(1)公式特征:第一个因数是,后面每一个因数比它前面一个少 1,最后一个因数是,共有个因数;( 2 ) 全 排 列 : 当时 即个 不 同 元 素 全 部 取 出 的 一 个 排 列 全 排 列 数 :(叫做 n 的阶乘)4、典例分析例 1.计算:(1); (2); (3).例 2.(1)若,则 , .(2)若则用排列数符号表示 .例 3.(1)从这五个数字中,任取 2 个数字组成分数,不同值的分数共有多少个?(2)5 人站成一排照相,共有多少种不同的站法?(3)某年全国足球甲级(A 组)联赛共有 14 队参加,每队都要与其余各队在主客场分别比赛 1 次,共进行多少场比赛?课堂小节:本节课学习了排列、排列数的概念,排列数公式的推导课堂练习: (1)解方程:A=140A;(2)解不等式:A>6A.第二课时 1.2 排列答案4、典例分析例 1.解:(1) ==3360 ;(2) ==72...