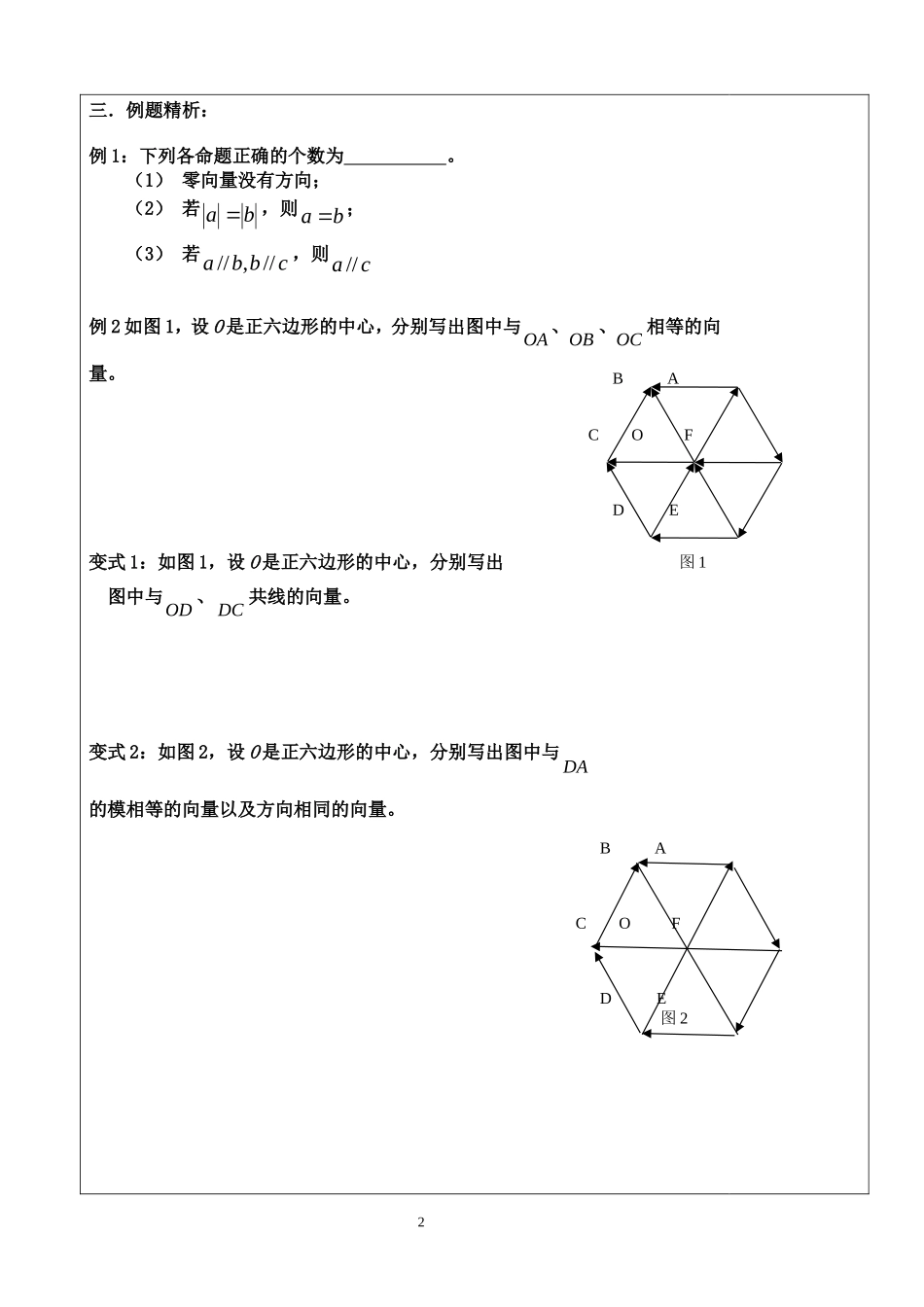
一体化教学案 主备人:总 课 题平 面 向 量第 1 课时课 题向量的概念及表示考纲要求理解并掌握向量、零向量、单位向量、相等向量、共线向量的概念,会表示向量.掌握平行向量、相等向量和共线向量的区别和联系.教学过程教 学 内 容一 知识点回顾 1.向量的定义: 。 2.向量的模: 。记作 。 3.零向量: 。记作 。 4.单位向量: 。 5.相等向量: 。 6.平行向量: 。 7.相反向量: 。 8.共线向量: 。二 课 前 预 习判断是非(1)平行向量一定方向相同 ( )(2)不相等的向量一定不平行 ( )(3)向量的模可以比较大小 ( )(4)平行的向量的方向一定相同 ( )(5)单位向量均相等 ( )(6)任一单位向量都大于0 ( )(7)共线向量一定在同一直线上 ( )1三.例题精析:例 1:下列各命题正确的个数为 。(1) 零向量没有方向;(2) 若ba ,则ba ;(3) 若cbba//,//,则ca//例 2 如图 1,设 O 是正六边形的中心,分别写出图中与OA�、OB�、OC�相等的向量。变式 1:如图 1,设 O 是正六边形的中心,分别写出图中与OD�、 DC�共线的向量。变式 2:如图 2,设 O 是正六边形的中心,分别写出图中与 DA�的模相等的向量以及方向相同的向量。 2 B AC O F D E图 1 B AC O F D E 图 23四.课堂练习: 1.下列命题是假命题的有 。(1) 向量 AB 的长度与向量 BA 的长度相等(2) 向量a 与b 平行,则a 与b 的方向相同或相反(3) 两个有共同起点且相等的向量,其终点必相同(4) 两个有公共终点的向量,一定是共线向量(5) 向量 AB 与向量CD 是共线向量,则点DCBA,,,必在 同一直线上 2.下列命题正确的是 。 ① 相等的向量就是模相等的向量② 方向不同的向量也可以相等③ 平行向量就是方向相等的向量④0与任何一向量平行 3.如右图,△ABC 中,D,E,F 分别是边 BC,AB,CA 的中点,在以 A、B、C、D、E、F为端点的有向线段中所表示的向量中,(1)与向量 FE�共线的有 .(2)与向量 DF�的模相等的有 .(3)与向量 ED�相等的有 . 4.在如图所示的向量edcba,,,,中(小正方形的边长为 1),是否存在:(1)共线向量?(2)相反向量?(3)相等向量?(4)模相等的向量? 若存在,分别写出这些向量。五.小 结4abcdeABCDEF五.课后总结:5