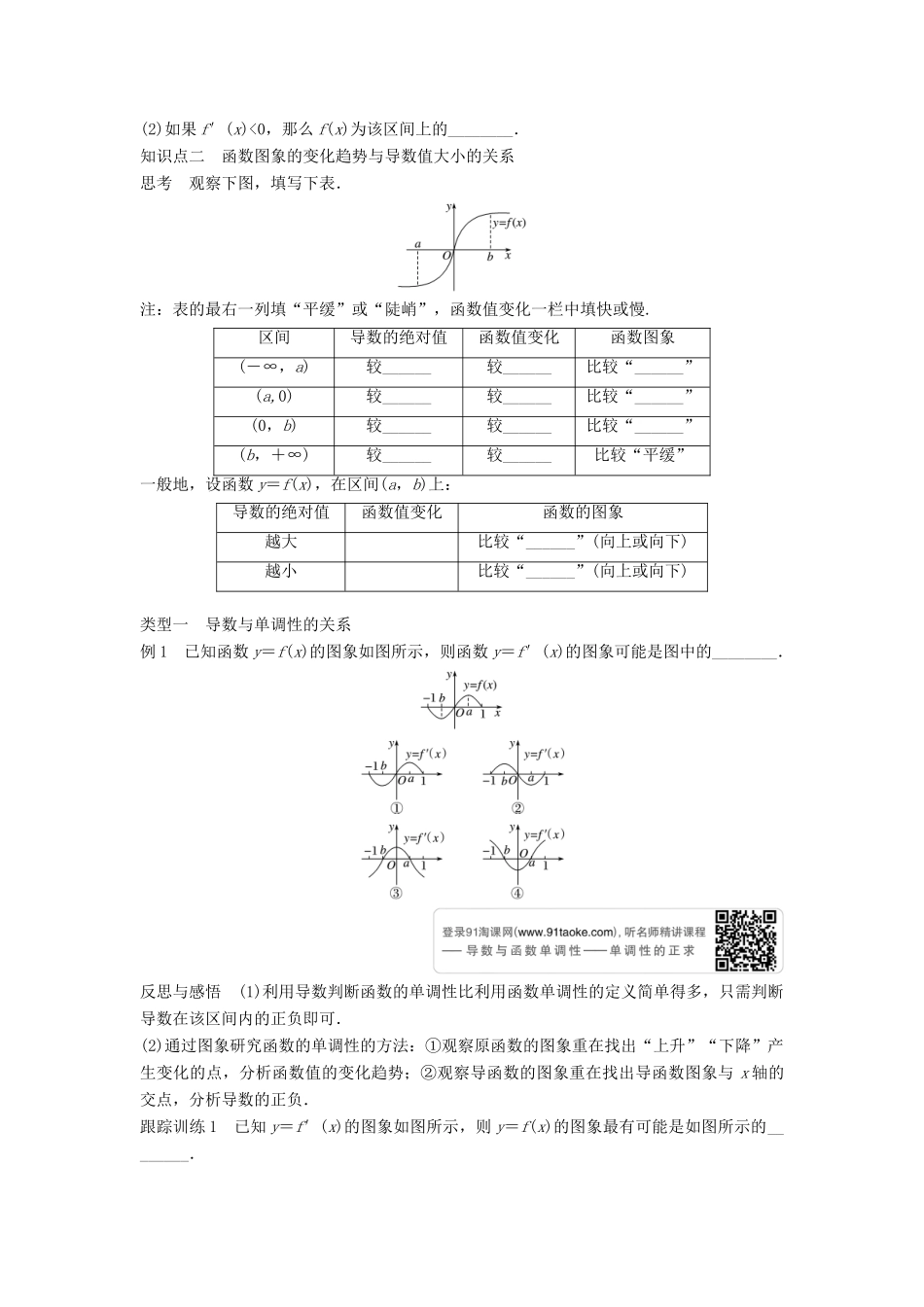
1.3.1 单调性学习目标 1.理解导数与函数的单调性的关系.2.掌握利用导数判断函数单调性的方法.3.能利用导数求不超过三次多项式函数的单调区间.知识点一 函数的单调性与导函数正负的关系思考 1 观察高台跳水运动员的高度 h 随时间 t 变化的函数 h(t)=-4.9t2+6.5t+10 的图象及 h′(t)=-9.8t+6.5 的图象,思考运动员从起跳到最高点,从最高点到入水的运动状态有什么区别. 思考 2 观察图中函数 f(x),填写下表.导数值切线的斜率切线倾斜角曲线的变化趋势函数的单调性>0____0____角<0____0____角一般地,设函数 y=f(x),在区间(a,b)上(1)如果 f′(x)>0,那么 f(x)为该区间上的________;(2)如果 f′(x)<0,那么 f(x)为该区间上的________.知识点二 函数图象的变化趋势与导数值大小的关系思考 观察下图,填写下表.注:表的最右一列填“平缓”或“陡峭”,函数值变化一栏中填快或慢.区间导数的绝对值函数值变化函数图象(-∞,a)较______较______比较“______”(a,0)较______较______比较“______”(0,b)较______较______比较“______”(b,+∞)较______较______比较“平缓”一般地,设函数 y=f(x),在区间(a,b)上:导数的绝对值函数值变化函数的图象越大比较“______”(向上或向下)越小比较“______”(向上或向下)类型一 导数与单调性的关系例 1 已知函数 y=f(x)的图象如图所示,则函数 y=f′(x)的图象可能是图中的________.反思与感悟 (1)利用导数判断函数的单调性比利用函数单调性的定义简单得多,只需判断导数在该区间内的正负即可.(2)通过图象研究函数的单调性的方法:①观察原函数的图象重在找出“上升”“下降”产生变化的点,分析函数值的变化趋势;②观察导函数的图象重在找出导函数图象与 x 轴的交点,分析导数的正负.跟踪训练 1 已知 y=f′(x)的图象如图所示,则 y=f(x)的图象最有可能是如图所示的________.类型二 利用导数研究函数的单调性例 2 讨论函数 f(x)=ax2+x-(a+1)ln x(a≥0)的单调性. 反思与感悟 (1)本题易忽略 a=0 的情况而致错,同时,求函数的单调性一定要注意函数的定义域.(2)利用导数研究函数单调性的方法:第一步:求定义域,对函数求导;第二步:解导数等于 0 时的方程;第三步:导数大于 0 的区间与定义域求交集为增区间,小于 0 的区间与定义域求交集为减区间,即“正增负减”.跟踪训练 2 设函数 f(x)=ex-ax-2,求 f(x)的单...