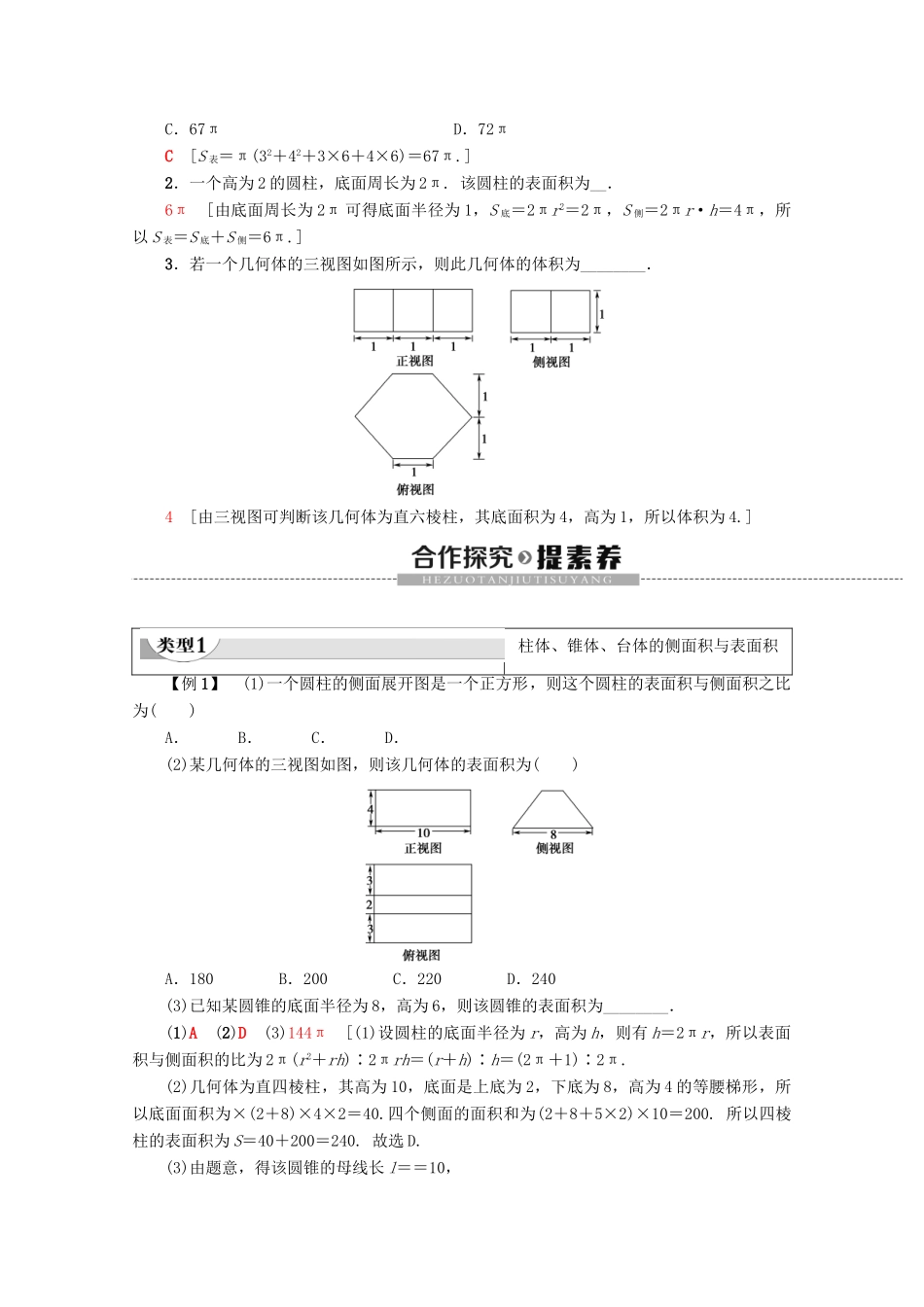
1.3.1 柱体、锥体、台体的表面积与体积学 习 目 标核 心 素 养1.通过对柱体、锥体、台体的研究,掌握柱体、锥体、台体的表面积与体积的求法.(重点)2.会求组合体的表面积与体积.(难点、易错点)通过学习并运用柱体、锥体、台体的表面积和体积公式,培养学生数学运算、直观想象、逻辑推理的数学素养.1.表面积公式(1)棱柱、棱锥、棱台的表面积图形表面积公式多面体多面体的表面积就是各个面的面积的和,也就是展开图的面积(2)旋转体的表面积旋转体圆柱底面积:S 底=π r 2 ;侧面积:S 侧=2π rl ;表面积:S=2π rl + 2π r 2 圆锥底面积:S 底=π r 2 ;侧面积:S 侧=π rl ;表面积:S=π rl + π r 2 圆台上底面面积:S 上底=π r ′ 2 ;下底面面积:S 下底=π r 2 ;侧面积:S 侧=π l ( r + r ′) ;表面积:S=π( r ′ 2 + r 2 + r ′ l + rl ) 2.体积公式(1)柱体:柱体的底面面积为 S,高为 h,则 V=Sh.(2)锥体:锥体的底面面积为 S,高为 h,则 V=Sh.(3)台体:台体的上、下底面面积分别为 S′,S,高为 h,则 V=( S ′ ++ S ) h .思考:简单组合体分割成几个几何体,其表面积不变吗?其体积呢?[提示] 表面积变大了,而体积不变.1.圆台的上、下底面半径分别为 3 和 4,母线长为 6,则其表面积等于( )A.72 B.42πC.67πD.72πC [S 表=π(32+42+3×6+4×6)=67π.]2.一个高为 2 的圆柱,底面周长为 2π. 该圆柱的表面积为__.6π [由底面周长为 2π 可得底面半径为 1,S 底=2πr2=2π,S 侧=2πr·h=4π,所以 S 表=S 底+S 侧=6π.]3.若一个几何体的三视图如图所示,则此几何体的体积为________.4 [由三视图可判断该几何体为直六棱柱,其底面积为 4,高为 1,所以体积为 4.]柱体、锥体、台体的侧面积与表面积【例 1】 (1)一个圆柱的侧面展开图是一个正方形,则这个圆柱的表面积与侧面积之比为( )A. B. C. D.(2)某几何体的三视图如图,则该几何体的表面积为( )A.180 B.200 C.220 D.240(3)已知某圆锥的底面半径为 8,高为 6,则该圆锥的表面积为________.(1)A (2)D (3)144π [(1)设圆柱的底面半径为 r,高为 h,则有 h=2πr,所以表面积与侧面积的比为 2π(r2+rh)∶2πrh=(r+h)∶h=(2π+1)∶2π.(2)几何体为直四棱柱,其高为 10,底面是上底...