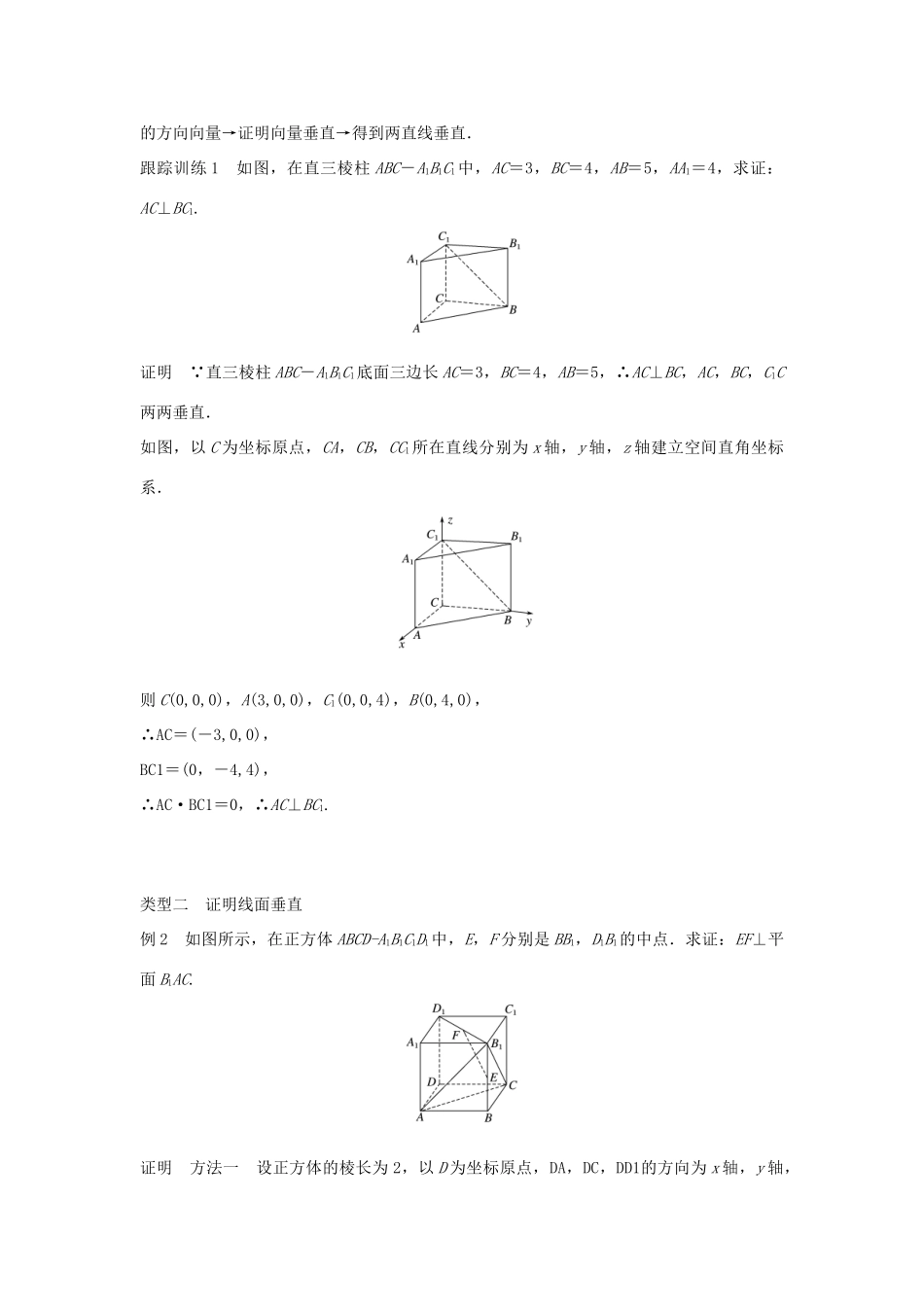
3.2.2 空间线面关系的判定(二)——垂直关系学习目标 1.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直关系.2.能用向量法判断一些简单的线线、线面、面面垂直关系.知识点一 向量法判断线线垂直设直线 l 的方向向量为 a=(a1,a2,a3),直线 m 的方向向量为 b=(b1,b2,b3),则l⊥m⇔a·b=0⇔a1b1+ a 2b2+ a 3b3= 0 .知识点二 向量法判断线面垂直思考 若直线 l 的方向向量为 μ1=,平面 α 的法向量为 μ2=,则直线 l 与平面 α 的位置关系是怎样的?如何用向量法判断直线与平面的位置关系?答案 垂直,因为 μ1=μ2,所以 μ1∥μ2,即直线的方向向量与平面的法向量平行,所以直线 l 与平面 α 垂直.判断直线与平面的位置关系的方法:(1)直线 l 的方向向量与平面 α 的法向量共线⇒l⊥α. (2)直线的方向向量与平面的法向量垂直⇒直线与平面平行或直线在平面内.(3)直线 l 的方向向量与平面 α 内的两相交直线的方向向量垂直⇒l⊥α.梳理 设直线 l 的方向向量 a=(a1,b1,c1),平面 α 的法向量 μ=(a2,b2,c2),则l⊥α⇔a∥μ⇔a=kμ(k∈R).知识点三 向量法判断面面垂直思考 平面 α,β 的法向量分别为 μ1=(x1,y1,z1),μ2=(x2,y2,z2),用向量坐标法表示两平面 α,β 垂直的关系式是什么?答案 x1x2+y1y2+z1z2=0.梳理 若平面 α 的法向量为 μ=(a1,b1,c1),平面 β 的法向量为 ν=(a2,b2,c2),则α⊥β⇔μ⊥ν⇔μ·ν=0⇔a1a2+ b 1b2+ c 1c2= 0 .已知点 P 是平行四边形 ABCD 所在的平面外一点,如果 AB=(2,-1,-4),AD=(4,2,0),AP=(-1,2,-1).判断下面结论的对错:1.AP⊥AB;(√)2.AP⊥AD.(√)3.AP是平面 ABCD 的法向量.(√)4.AP∥BD.(×)类型一 证明线线垂直例 1 如图,已知正三棱柱 ABC-A1B1C1的各棱长都为 1,M 是底面上 BC 边的中点,N 是侧棱CC1上的点,且 CN=CC1.求证:AB1⊥MN.证明 设 AB 的中点为 O,连结 OC,作 OO1∥AA1.以 O 为坐标原点,OB 所在直线为 x 轴,OC所在直线为 y 轴,OO1所在直线为 z 轴建立如图所示的空间直角坐标系.由已知得 A,B,C,N,B1, M 为 BC 的中点,∴M.∴MN=,AB1=(1,0,1),∴MN·AB1=-+0+=0.∴MN⊥AB1,∴AB1⊥MN.反思与感悟 证明两直线垂直的基本步骤:建立空间直角坐标系→写出点的坐标→求直线的方向向量→...