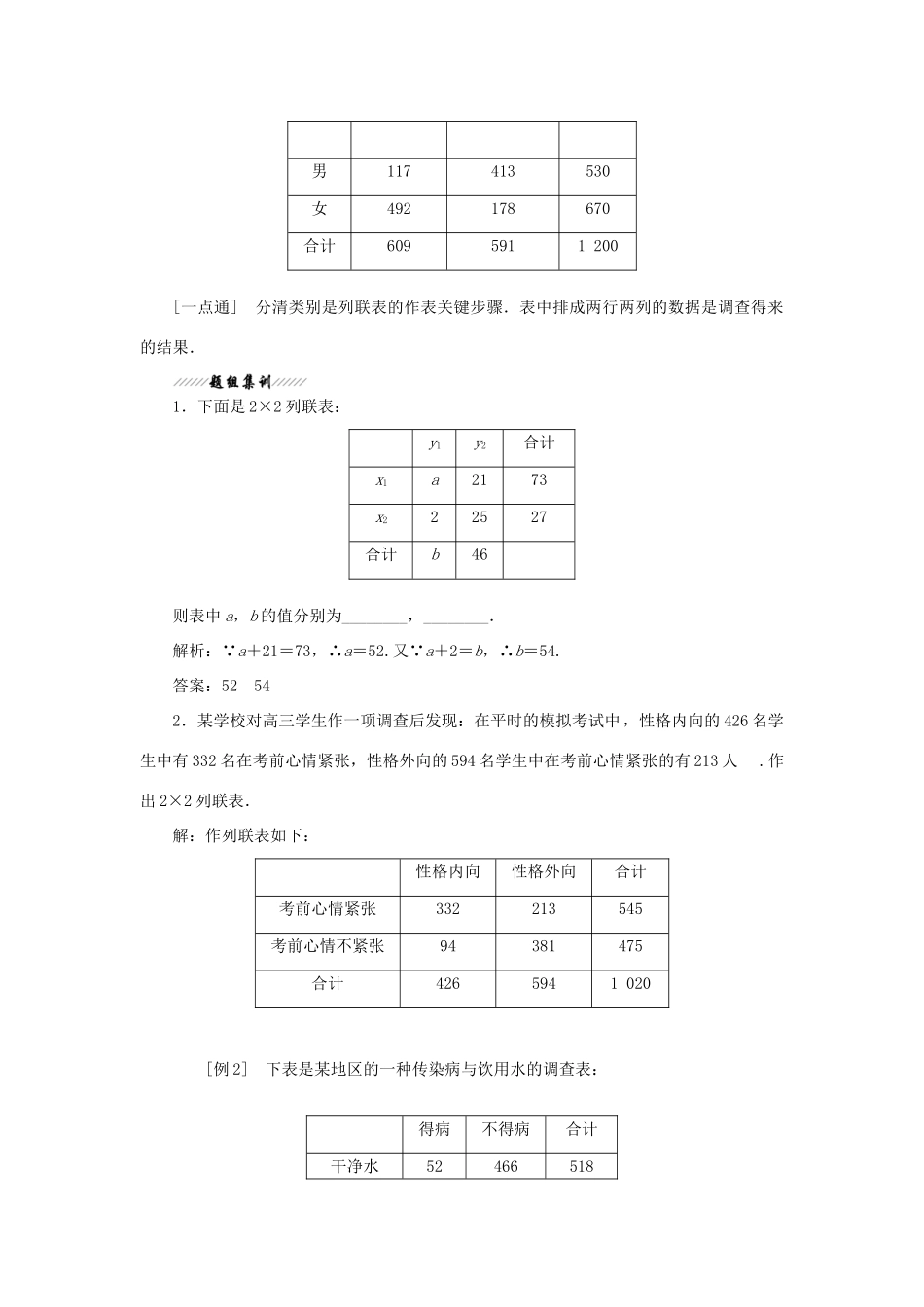
3.1 独立性检验1.2×2 列联表的定义对于两个研究对象Ⅰ和Ⅱ,Ⅰ有两类取值,即类 A 和类 B;Ⅱ也有两类取值,即类 1 和类 2.这些取值可用下面的 2×2 列联表表示. 2.χ2统计量的求法公式 χ2=.3.独立性检验的概念用统计量 χ 2 研究两变量是否有关的方法称为独立性检验.4.独立性检验的步骤要判断“Ⅰ与Ⅱ有关系”,可按下面的步骤进行:(1)提出假设 H0:Ⅰ与Ⅱ没有关系;(2)根据 2×2 列联表及 χ2公式,计算的值;(3)查对临界值,作出判断.其中临界值如表所示:P(χ2≥x0)0.500.400.250.150.100.050.0250.0100.0050.001χ00.4550.7081.3232.0722.7063.8415.0246.6357.87910.828 表示在 H0成立的情况下,事件“χ2≥x0”发生的概率.5.变量独立性判断的依据(1)如果>10.828 时,那么有 99.9%的把握认为“Ⅰ与Ⅱ有关系”;(2)如果>6.635 时,那么有 99%的把握认为“Ⅰ与Ⅱ有关系”;(3)如果>2.706 时,那么有 90%的把握认为“Ⅰ与Ⅱ有关系”;(4)如果≤ 2.706 时,那么就认为没有充分的证据显示“Ⅰ与Ⅱ有关系”,但也不能作出结论“H0成立”,即Ⅰ与Ⅱ没有关系.1.在 2×2 列联表中,通常要求 a,b,c,d 的值均不小于 5.2.表中|ad-bc|越小,Ⅰ与Ⅱ关系越弱;|ad-bc|越大,Ⅰ与Ⅱ关系越强.同时要记准表中 a,b,c,d 四个数据是交叉相乘然后再作差取绝对值,一定不要乘错.3.表中类 A 与类 B,以及类 1 与类 2 的关系:对于对象Ⅰ来说,类 A 与类 B 是对立的,也就是说类 A 发生,类 B 一定不发生,类 A 不发生,则类 B 一定发生;同样对于对象Ⅱ来说,类 1 与类 2 的关系也是如此. [例 1] 在一项有关医疗保健的社会调查中,发现调查的男性为 530 人,女性为670 人,其中男性中喜欢吃甜食的为 117 人,女性中喜欢吃甜食的为 492 人,请作出性别与喜欢吃甜食的列联表.[思路点拨] 在 2×2 列联表中,共有两类变量,每一类变量都有两个不同的取值,然后找出相应的数据,列表即可.[精解详析] 作列联表如下:喜欢甜食不喜欢甜食合计男117413530女492178670合计6095911 200[一点通] 分清类别是列联表的作表关键步骤.表中排成两行两列的数据是调查得来的结果.1.下面是 2×2 列联表:y1y2合计x1a2173x222527合计b46则表中 a,b 的值分别为________,________.解析: a+21=73,∴a=52.又 a+2=b,∴b=54.答案:52 542.某学校对高三学生作一项...