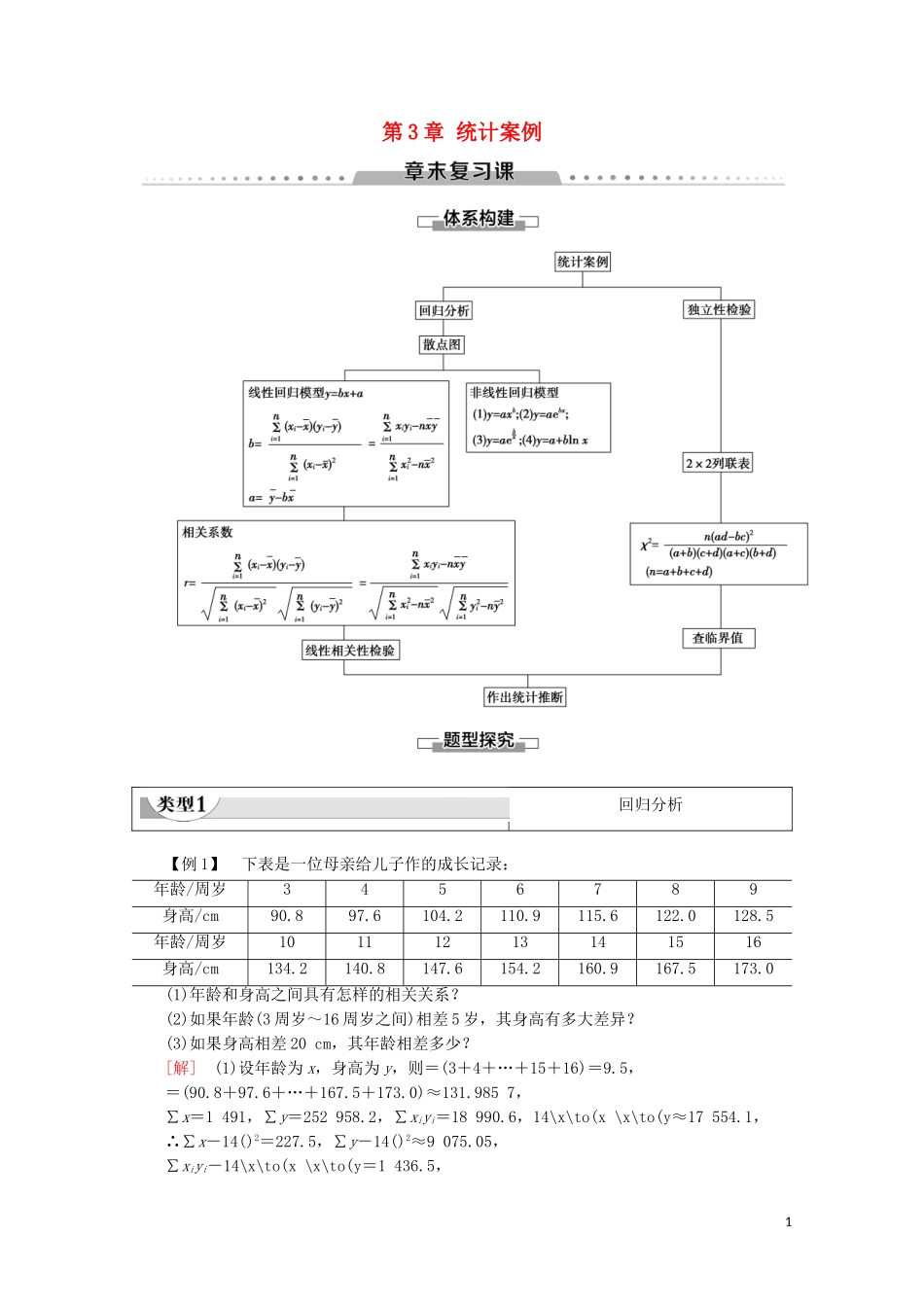
第 3 章 统计案例回归分析【例 1】 下表是一位母亲给儿子作的成长记录:年龄/周岁3456789身高/cm90.897.6104.2110.9115.6122.0128.5年龄/周岁10111213141516身高/cm134.2140.8147.6154.2160.9167.5173.0(1)年龄和身高之间具有怎样的相关关系?(2)如果年龄(3 周岁~16 周岁之间)相差 5 岁,其身高有多大差异?(3)如果身高相差 20 cm,其年龄相差多少?[解] (1)设年龄为 x,身高为 y,则=(3+4+…+15+16)=9.5,=(90.8+97.6+…+167.5+173.0)≈131.985 7,∑x=1 491,∑y=252 958.2,∑xiyi=18 990.6,14\x\to(x \x\to(y≈17 554.1,∴∑x-14()2=227.5,∑y-14()2≈9 075.05,∑xiyi-14\x\to(x \x\to(y=1 436.5,1∴r==≈0.999 7.因此,年龄和身高之间具有较强的线性相关关系.(2)由(1)得 b==≈6.314,a=-b=131.985 7-6.314×9.5≈72,∴x 与 y 的线性回归方程为 y=6.314x+72.因此,如果年龄相差 5 岁,那么身高相差 6.314×5=31.57(cm).(3)如果身高相差 20 cm,年龄相差≈3.168≈3(岁).解决回归分析问题的一般步骤1画散点图.根据已知数据画出散点图.2判断变量的相关性并求回归方程.通过观察散点图,直观感知两个变量是否具有相关关系;在此基础上,利用最小二乘法求回归系数,然后写出回归方程.3实际应用.依据求得的回归方程解决实际问题.1.某运动员训练次数与运动成绩之间的数据关系如下:次数 x3033353739444650成绩 y3034373942464851(1)作出散点图;(2)求出回归直线方程;(3)计算相关系数并进行相关性检验;(4)试预测该运动员训练 47 次及 55 次的成绩.[解] (1)作出该运动员训练次数 x 与成绩 y 之间的散点图,如图所示,由散点图可知,它们之间具有线性相关关系.(2)列表计算:次数 xi成绩 yixyxiyi303090090090033341 0891 1561 12235371 2251 3691 29537391 3691 5211 44339421 5211 7641 63844461 9362 1162 02446482 1162 3042 20850512 5002 6012 550由上表可求得=39.25,=40.875,2=12 656,=13 731,iyi=13 180,∴b=≈1.041 5,a=-b=-0.003 88,∴回归直线方程为 y=1.041 5x-0.003 88.(3)计算相关系数 r=0.992 7,因此运动员的成绩和训练次数两个变量有较强的相关关系.(4)由上述分析可知,我们可用回归直线方程 y=1.041 5x-0.003 88 作为该运动员成绩的预报值.将 x=47 和 x=55...