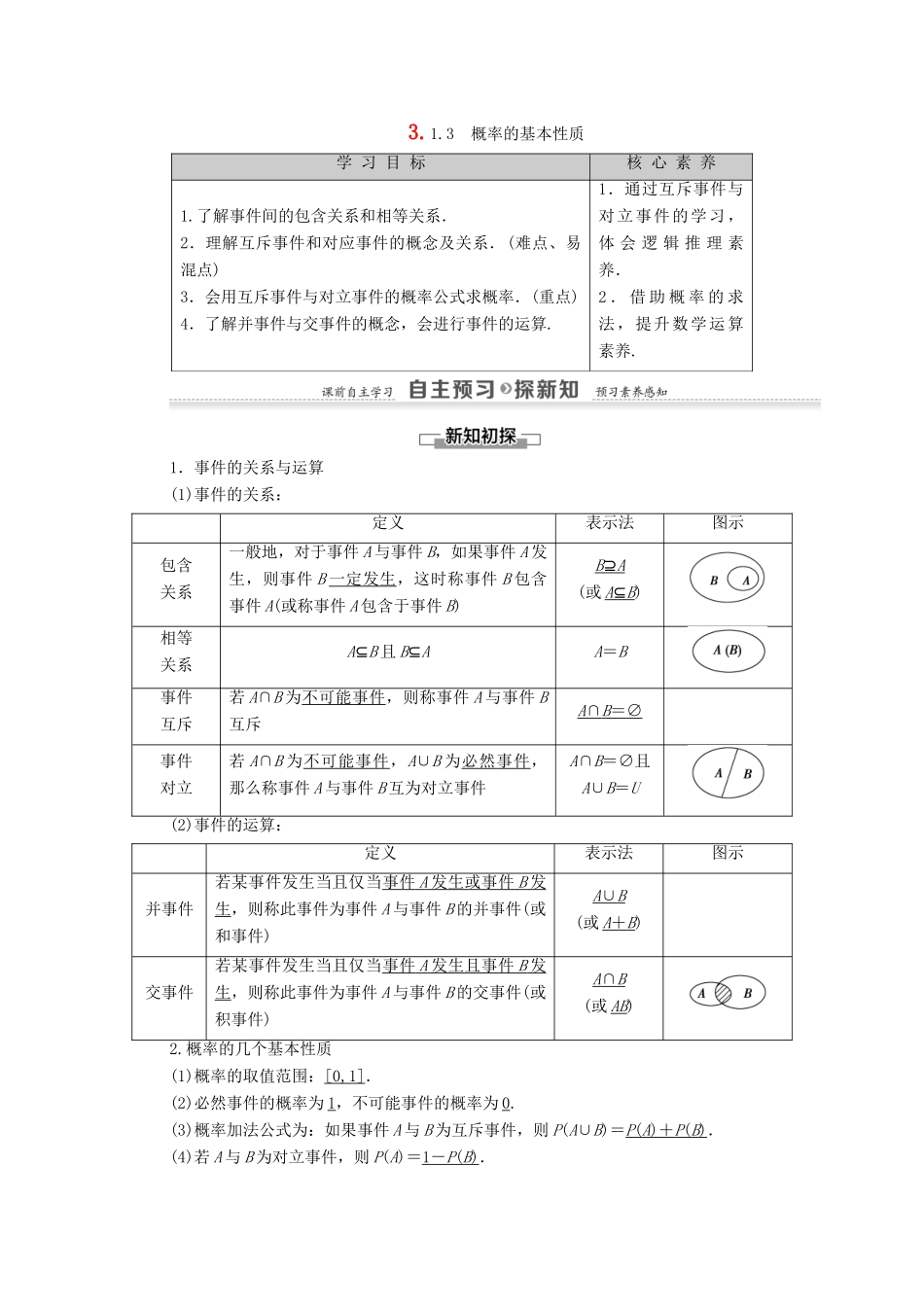
3.1.3 概率的基本性质学 习 目 标核 心 素 养1.了解事件间的包含关系和相等关系.2.理解互斥事件和对应事件的概念及关系.(难点、易混点)3.会用互斥事件与对立事件的概率公式求概率.(重点)4.了解并事件与交事件的概念,会进行事件的运算.1.通过互斥事件与对立事件的学习,体 会 逻 辑 推 理 素养.2 . 借 助 概 率 的 求法,提升数学运算素养.1.事件的关系与运算(1)事件的关系:定义表示法图示包含关系一般地,对于事件 A 与事件 B,如果事件 A 发生,则事件 B 一定发生,这时称事件 B 包含事件 A(或称事件 A 包含于事件 B)B ⊇ A (或 A ⊆ B )相等关系A⊆B 且 B⊆AA=B事件互斥若 A∩B 为不可能事件,则称事件 A 与事件 B互斥A ∩ B = ∅ 事件对立若 A∩B 为不可能事件,A∪B 为必然事件,那么称事件 A 与事件 B 互为对立事件A∩B=∅且A∪B=U(2)事件的运算:定义表示法图示并事件若某事件发生当且仅当事件 A 发生或事件 B 发 生,则称此事件为事件 A 与事件 B 的并事件(或和事件)A ∪ B (或 A + B )交事件若某事件发生当且仅当事件 A 发生且事件 B 发 生,则称此事件为事件 A 与事件 B 的交事件(或积事件)A ∩ B (或 AB)2.概率的几个基本性质(1)概率的取值范围:[0,1].(2)必然事件的概率为 1,不可能事件的概率为 0.(3)概率加法公式为:如果事件 A 与 B 为互斥事件,则 P(A∪B)=P ( A ) + P ( B ) .(4)若 A 与 B 为对立事件,则 P(A)=1 - P ( B ) .P(A∪B)=1,P(A∩B)=0.思考:在掷骰子的试验中,事件 A={出现的点数为 1},事件 B={出现的点数为奇数}A 与 B 应有怎样的关系?[提示] A⊆B1.同时掷两枚硬币,向上面都是正面为事件 A,向上面至少有一枚是正面为事件 B,则有( )A.A⊆B B.A⊇BC.A=BD.A