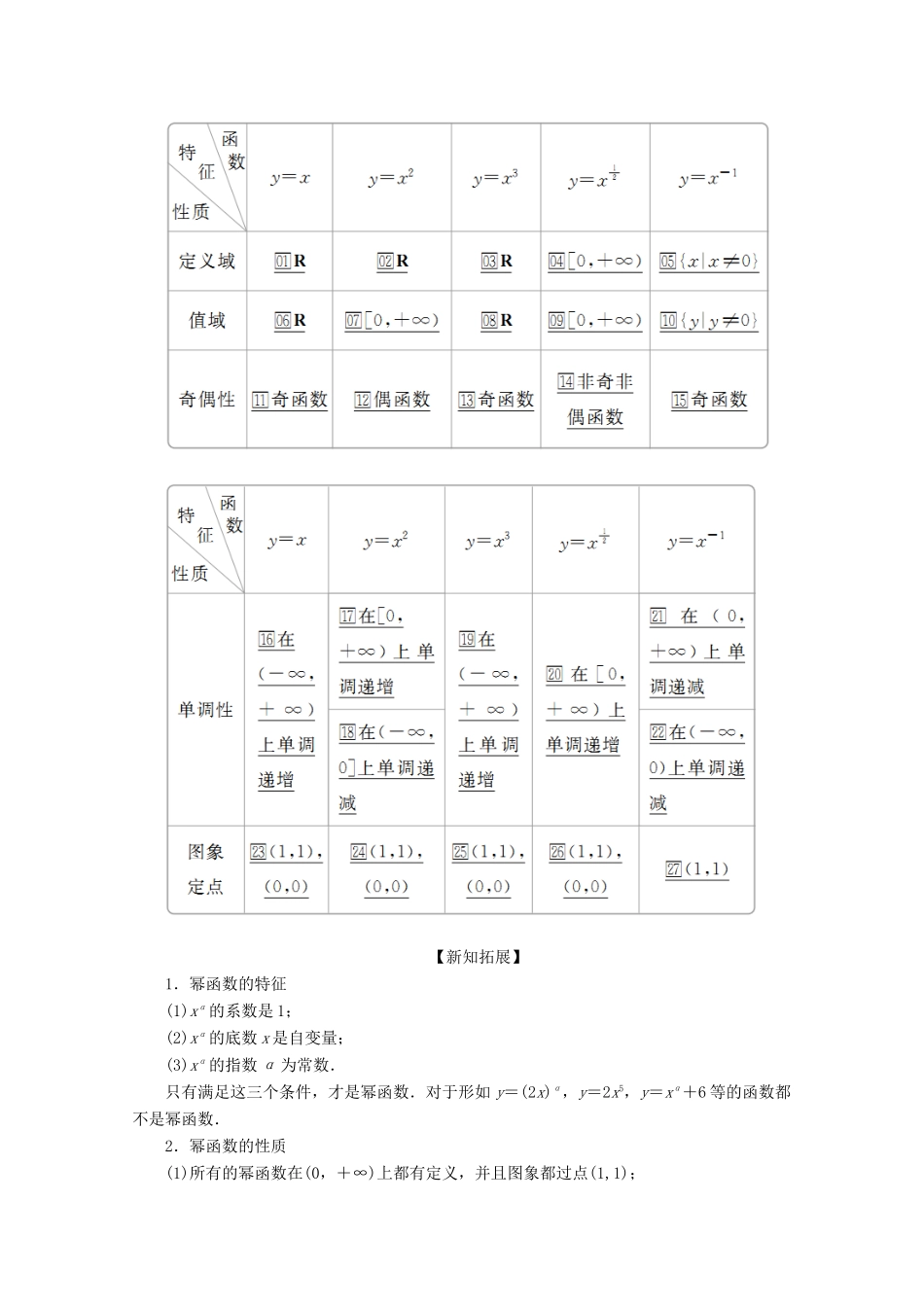
3.3 幂函数(教师独具内容)课程标准:1.通过具体实例了解幂函数的概念.2.会画幂函数 y=x,y=x2,y=x3,y=,y=x的图象,并能通过图象了解幂函数的图象与性质.3.能正确应用幂函数的知识解决相关问题.教学重点:1.幂函数的概念.2.幂函数的图象与性质.教学难点:应用幂函数的知识解决相关问题.【知识导学】知识点一 幂函数的概念一般地,函数□ y = x α 叫做幂函数(power function),其中□ x 是自变量,□ α 是常数.知识点二 一些常用幂函数的图象同一坐标系中,幂函数 y=x,y=x2,y=x3,y=x-1,y=x的图象(如图).知识点三 一些常用幂函数的性质【新知拓展】1.幂函数的特征(1)xα的系数是 1;(2)xα的底数 x 是自变量;(3)xα的指数 α 为常数.只有满足这三个条件,才是幂函数.对于形如 y=(2x)α,y=2x5,y=xα+6 等的函数都不是幂函数.2.幂函数的性质(1)所有的幂函数在(0,+∞)上都有定义,并且图象都过点(1,1);(2)如果 α>0,那么幂函数的图象过原点,并且在区间[0,+∞)上单调递增;(3)如果 α<0,那么幂函数的图象在区间(0,+∞)上单调递减,在第一象限内,当 x从右边趋向于原点时,图象在 y 轴右方无限接近 y 轴,当 x 从原点趋向于+∞时,图象在 x轴上方无限接近 x 轴;(4)在(1,+∞)上,随幂指数的逐渐增大,图象越来越靠近 y 轴.1.判一判(正确的打“√”,错误的打“×”)(1)函数 y=x3+2 是幂函数.( )(2)幂函数的图象必过(0,0)和(1,1)这两点.( )(3)幂函数 y=xα的定义域为 R,与指数无关.( )(4)当 x>1 时,函数 y=x2的图象总在函数 y=x3的图象的下方.( )答案 (1)× (2)× (3)× (4)√2.做一做(请把正确的答案写在横线上)(1)若 y=mxα+(2n-4)是幂函数,则 m+n=________.(2)已知幂函数 f(x)=xα的图象经过点(2,8),则 f(-2)=________.(3)若 y=ax是幂函数,则该函数的值域是________.答案 (1)3 (2)-8 (3)[0,+∞) 题型一 幂函数的定义例 1 已知幂函数 y=(m2-m-1)xm2-2m-3,求此幂函数的解析式,并指出其定义域.[解] y=(m2-m-1)xm2-2m-3为幂函数,∴m2-m-1=1,解得 m=2 或 m=-1.当 m=2 时,m2-2m-3=-3,则 y=x-3,且有 x≠0;当 m=-1 时,m2-2m-3=0,则 y=x0,且有 x≠0.故所求幂函数的解析式为 y=x-3或 y=x0,它们的定义域都是{x|x≠0}.金版点睛判断函数是幂...