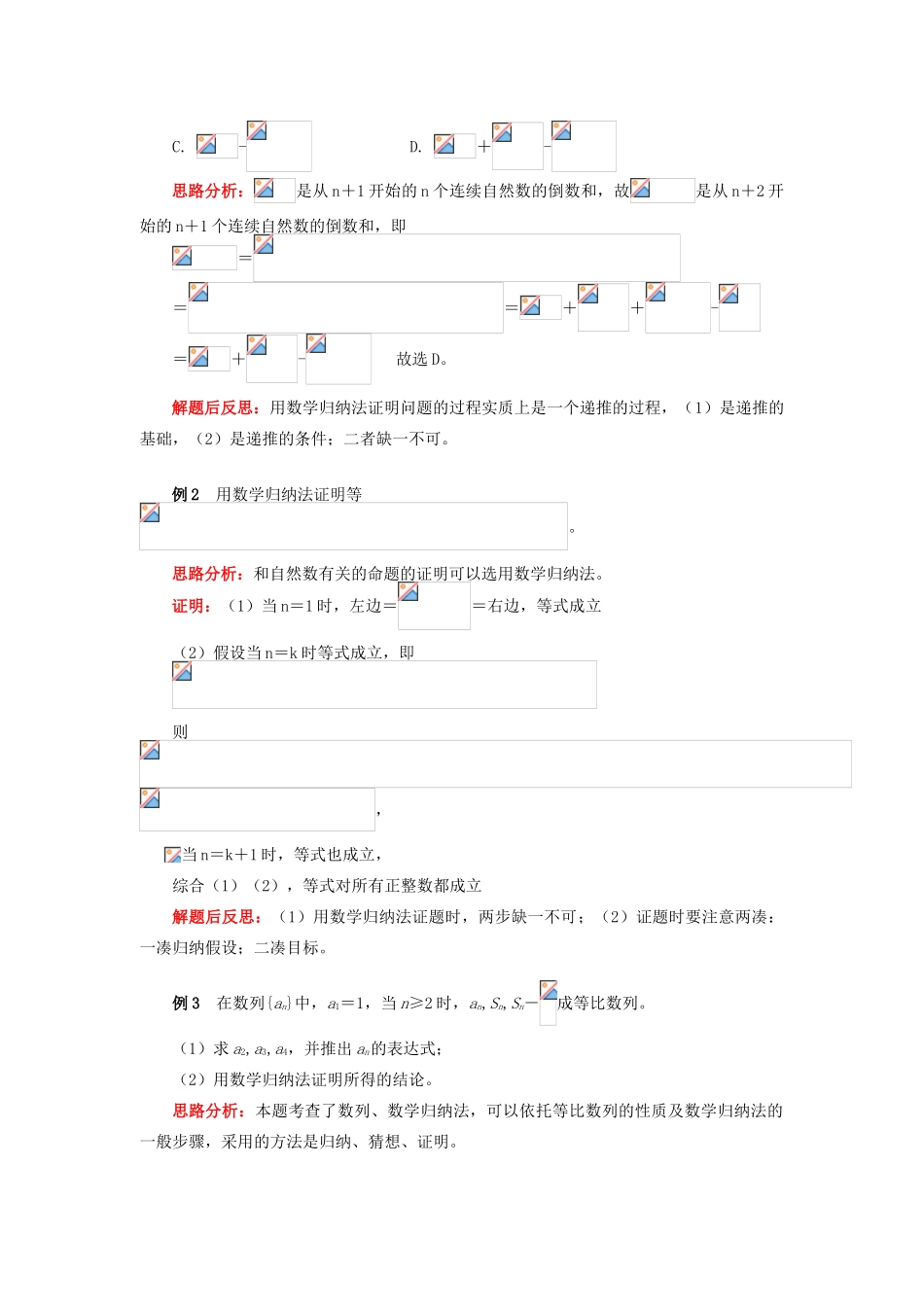
第 3 节 数学归纳法一、学习目标:了解数学归纳法的原理,会用数学归纳法证明与自然数有关的命题。 二、重点、难点能运用数学归纳法证明和自然数有关的命题。三、考点分析:数学归纳法中的归纳思想是比较常见的数学思想,因此要重视。数学归纳法在考试中时隐时现,且较隐蔽,因此在复习中应引起重视。只要与自然数有关,都可考虑使用数学归纳法,当然主要是恒等式、等式、不等式、整除问题、几何问题、三角问题、数列问题等联系得更多一些。一、数学归纳法的定义:由归纳法得到的与自然数有关的数学命题常采用下面的证明方法:(1)先证明当 n=n0(n0是使命题成立的最小自然数)时命题成立;(2)假设当 n=k(k∈N*, k≥n0)时命题成立,再证明当 n=k+1 时命题也成立,那么就证明这个命题成立,这种证明方法叫数学归纳法。二、数学归纳法的应用:(1)证恒等式;(2)整除性的证明;(3)探求平面几何中的问题;(4)探求数列的通项;(5)不等式的证明。特别提示(1)用数学归纳法证题时,两步缺一不可;(2)证题时要注意两凑:一凑归纳假设;二凑目标。例 1 已知,则的值为( )A. + B. ++C. - D. +-思路分析:是从 n+1 开始的 n 个连续自然数的倒数和,故是从 n+2 开始的 n+1 个连续自然数的倒数和,即===++-=+- 故选 D。解题后反思:用数学归纳法证明问题的过程实质上是一个递推的过程,(1)是递推的基础,(2)是递推的条件;二者缺一不可。例 2 用数学归纳法证明等。思路分析:和自然数有关的命题的证明可以选用数学归纳法。证明:(1)当 n=1 时,左边==右边,等式成立 (2)假设当 n=k 时等式成立,即 则,当 n=k+1 时,等式也成立,综合(1)(2),等式对所有正整数都成立解题后反思:(1)用数学归纳法证题时,两步缺一不可;(2)证题时要注意两凑:一凑归纳假设;二凑目标。例 3 在数列{an}中,a1=1,当 n≥2 时,an,Sn,Sn-成等比数列。(1)求 a2,a3,a4,并推出 an的表达式;(2)用数学归纳法证明所得的结论。思路分析:本题考查了数列、数学归纳法,可以依托等比数列的性质及数学归纳法的一般步骤,采用的方法是归纳、猜想、证明。求通项可先证明{}是以为首项,为公差的等差数列,进而求得通项公式 解题过程: an,Sn,Sn-成等比数列,∴Sn2=an·(Sn-)(n≥2) (*)(1)由 a1=1,S2=a1+a2=1+a2,代入(*)式得 a2=-由 a1=1,a2=-,S3...