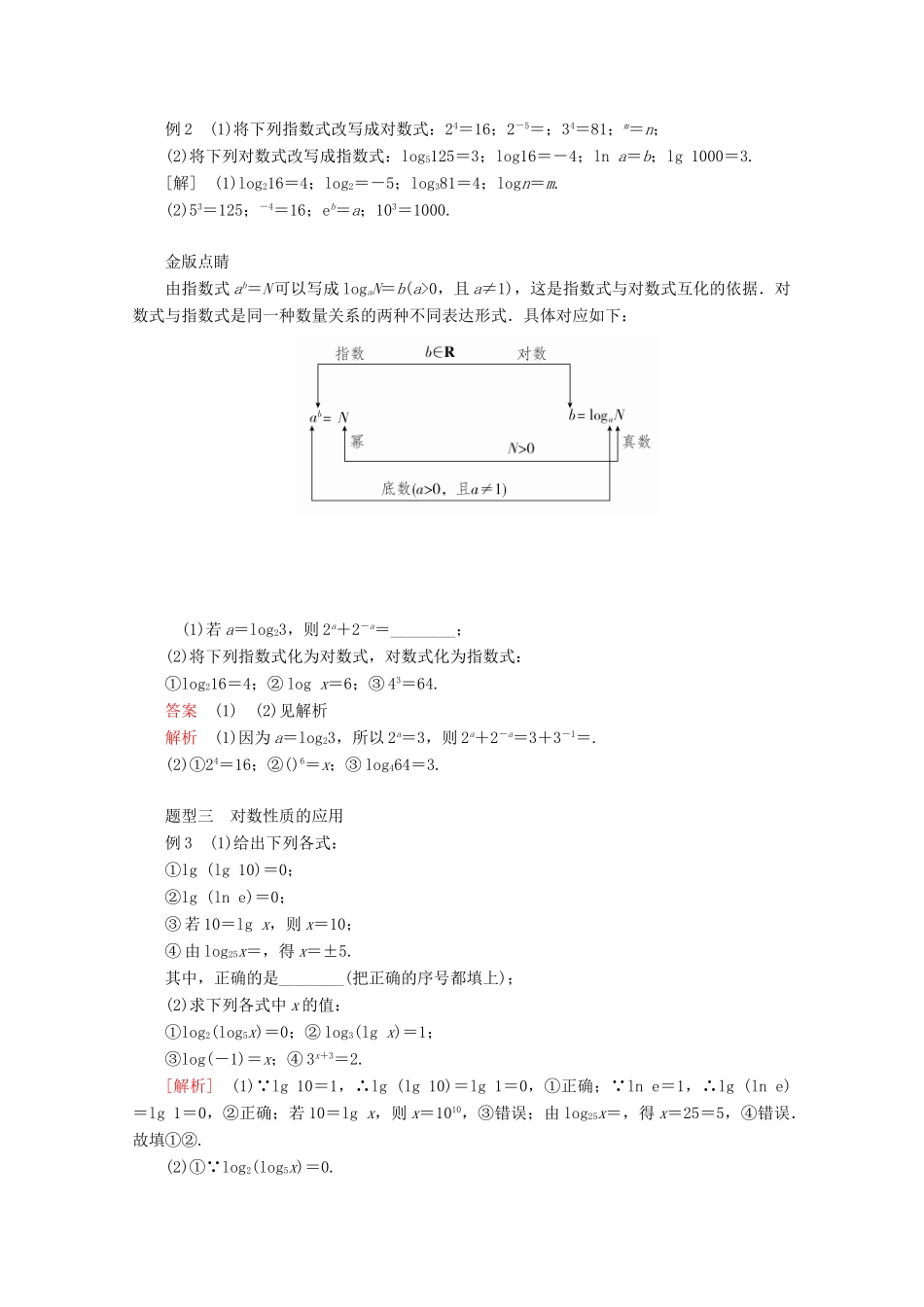
4.3.1 对数的概念(教师独具内容)课程标准:通过具体实例,理解对数的概念,了解常用对数与自然对数.理解对数的简单性质.教学重点:1.对数的概念,指数式与对数式的互化.2.对数的简单性质.教学难点:对数概念的理解,指数式与对数式之间的熟练转化.【知识导学】知识点一 对数的概念(1)对数的概念:如果□ a x = N (a>0,且 a≠1),那么数□ x 叫做以□ a 为底□ N 的对数,记作□x=logaN,其中□ a 叫做对数的底数,□ N 叫做真数.(2)两种特殊的对数① 常用对数:通常□ 以 10 为底 的对数叫做常用对数,N 的常用对数 log10N 简记为□ lg _N;② 自然对数:□ 以 e 为底 的对数称为自然对数,N 的自然对数 logeN 简记为□ ln _N(其中e=2.71828…).知识点二 对数与指数的关系(1)对数的基本性质①□ 零和负数 没有对数,即真数 N>0;②1 的对数为□ 0 ,即 loga1=□ 0 (a>0,且 a≠1);③ 底数的对数等于□ 1 ,即 logaa=□ 1 (a>0,且 a≠1).(2)两个重要的对数恒等式①alogaN=□ N (a>0,且 a≠1,N>0);②logaaN=□ N (a>0,且 a≠1).【新知拓展】在对数的概念中为什么规定 a>0 且 a≠1(1)若 a<0,则当 N 为某些值时,x 的值不存在,如:x=log(-2)8 不存在.(2)若 a=0,① 当 N≠0 时,x 的值不存在.如:log03(可理解为 0 的多少次幂是 3)不存在;② 当 N=0 时,x 可以是任意正实数,是不唯一的,即 log00 有无数个值.(3)若 a=1,① 当 N≠1 时,x 的值不存在.如:log13 不存在;② 当 N=1 时,x 可以为任意实数,是不唯一的,即 log11 有无数个值.因此规定 a>0,且 a≠1.1.判一判(正确的打“√”,错误的打“×”)(1)因为(-2)4=16,所以 log(-2)16=4.( )(2)对数式 log32 与 log23 的意义一样.( )(3)对于同一个正数,当底不同时,它的对数也不相同.( )(4)等式 loga1=0 对于任意实数 a 恒成立.( )答案 (1)× (2)× (3)× (4)×2.做一做(请把正确的答案写在横线上)(1)若 5x=2019,则 x=________.(2)lg 10=________;ln e=________.(3)将 log3a=2 化为指数式为________.答案 (1)log52019 (2)1 1 (3)32=a题型一 对数的概念例 1 (1)使对数 log2(-2x+1)有意义的 x 的取值范围为( )A. B.C. D.(2)在对数式 b=loga-2(5-a)中,实数 a 的取值范围是( )A.a>5 或...