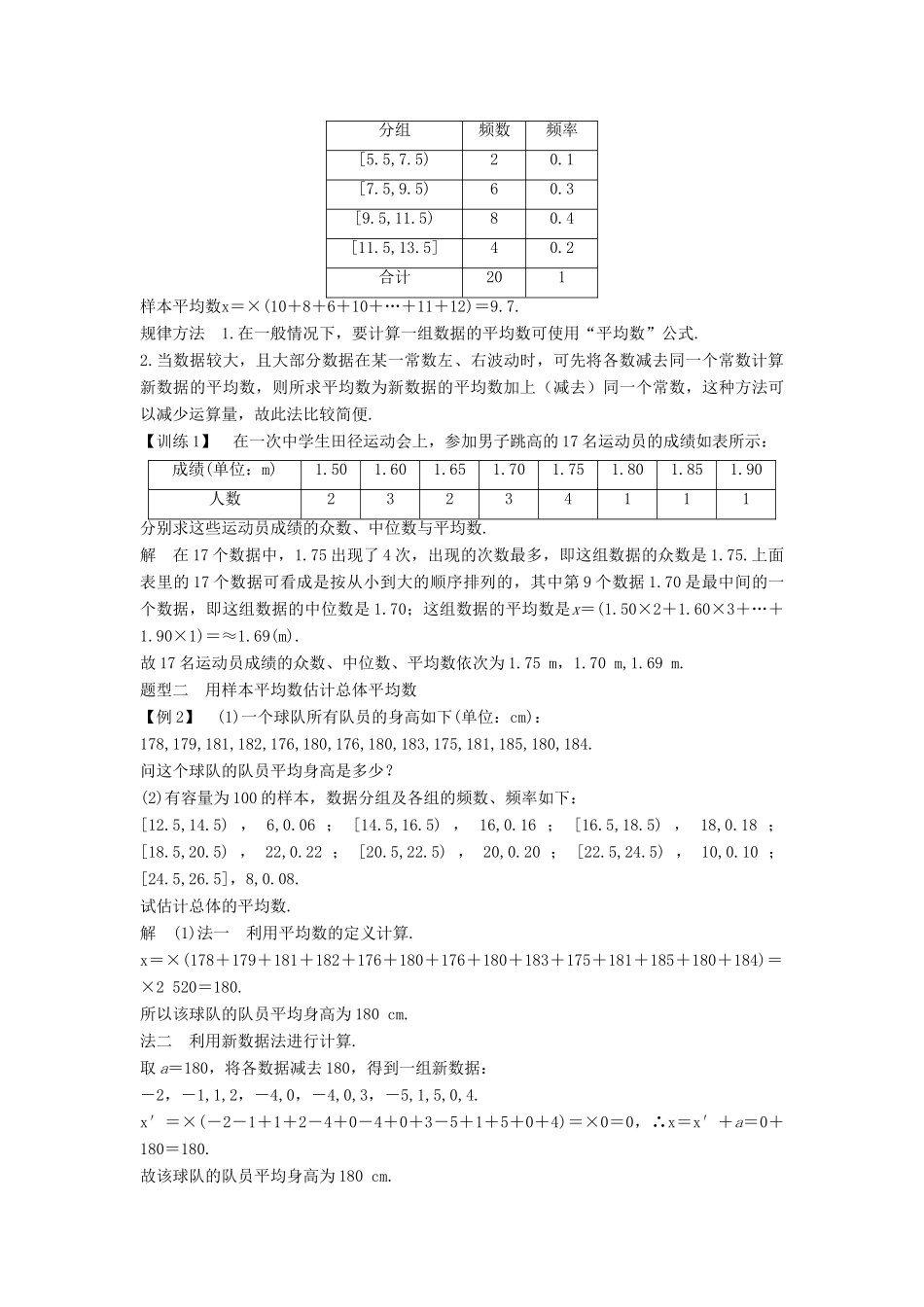
2.3.1 平均数及其估计内容要求 1.会求样本的平均数(重点);2.运用样本的平均数来估计总体的平均水平(重点);3.会应用相关知识解决简单的实际问题(难点).知识点 众数、中位数、平均数(或均值)1.众数、中位数、平均数(或均值)定义(1)众数:一组数据中重复出现次数最多的数.(2)中位数:把一组数据按从小到大的顺序排列,处在中间位置(或中间两个数的平均数)的数叫做这组数据的中位数.(3)平均数(或均值):如果 n 个数 x1,x2,…,xn,那么x=(x1+x2+…+xn)叫做这 n 个数的平均数(或均值).2.若取值为 x1,x2,…,xn的频率分别为 p1,p2,…,pn,则其平均数为 x1p1+ x 2p2+…+xnpn.3.三种数字特征与频率分布直方图的关系众数众数是最高长方形的中点所对应的数据,表示样本数据的中心值中位数(1)在频率分布直方图中,中位数左边和右边的直方图面积相等,由此可以估计中位数的值,但是有偏差;(2)表示样本数据所占频率的等分线平均数(1)平均数等于每个小矩形的面积乘以小矩形底边中点的横坐标之和;(2)平均数是频率分布直方图的重心,是频率分布直方图的平衡点【预习评价】对 某 商 店 一 个 月 内 每 天 的 顾 客 人 数 进 行 了 统 计 , 得 到 样 本 为(12,15,20,22,23,23,31,32,34,34,38,39,45,45,45,47,47,48,48,49,50,50,51,51,54,57,59,61,67,68),则该样本的中位数、众数、平均数分别是________.解析 由题意知各数为 12,15,20,22,23,23,31,32,34,34,38,39,45,45,45,47,47,48,48,49,50,50,51,51,54,57,59,61,67,68,中位数是 46,众数是 45,最大数为 68,最小数为12,平均数为 42.2.答案 46,45,42.2题型一 平均数的计算【例 1】 已知样本数据:10,8,6,10,8,13,10,10,10,7,8,9,12,8,11,12,9,10,11,12,列出频率分布表,求样本平均数.解 极差为 13-6=7,取组距为 2,分成 4 组,即[5.5,7.5),[7.5,9.5),[9.5,11.5),[11.5,13.5],列频率分布表如下:分组频数频率[5.5,7.5)20.1[7.5,9.5)60.3[9.5,11.5)80.4[11.5,13.5]40.2合计201样本平均数x=×(10+8+6+10+…+11+12)=9.7.规律方法 1.在一般情况下,要计算一组数据的平均数可使用“平均数”公式.2.当数据较大,且大部分数据在某一常数左、右波动时,可先将各数减去同一个常数计算新数据的平均数,则所求平均数为新数据的平均数加上(减去)同一个常数,这种方法可以减少运算量,故此法比...