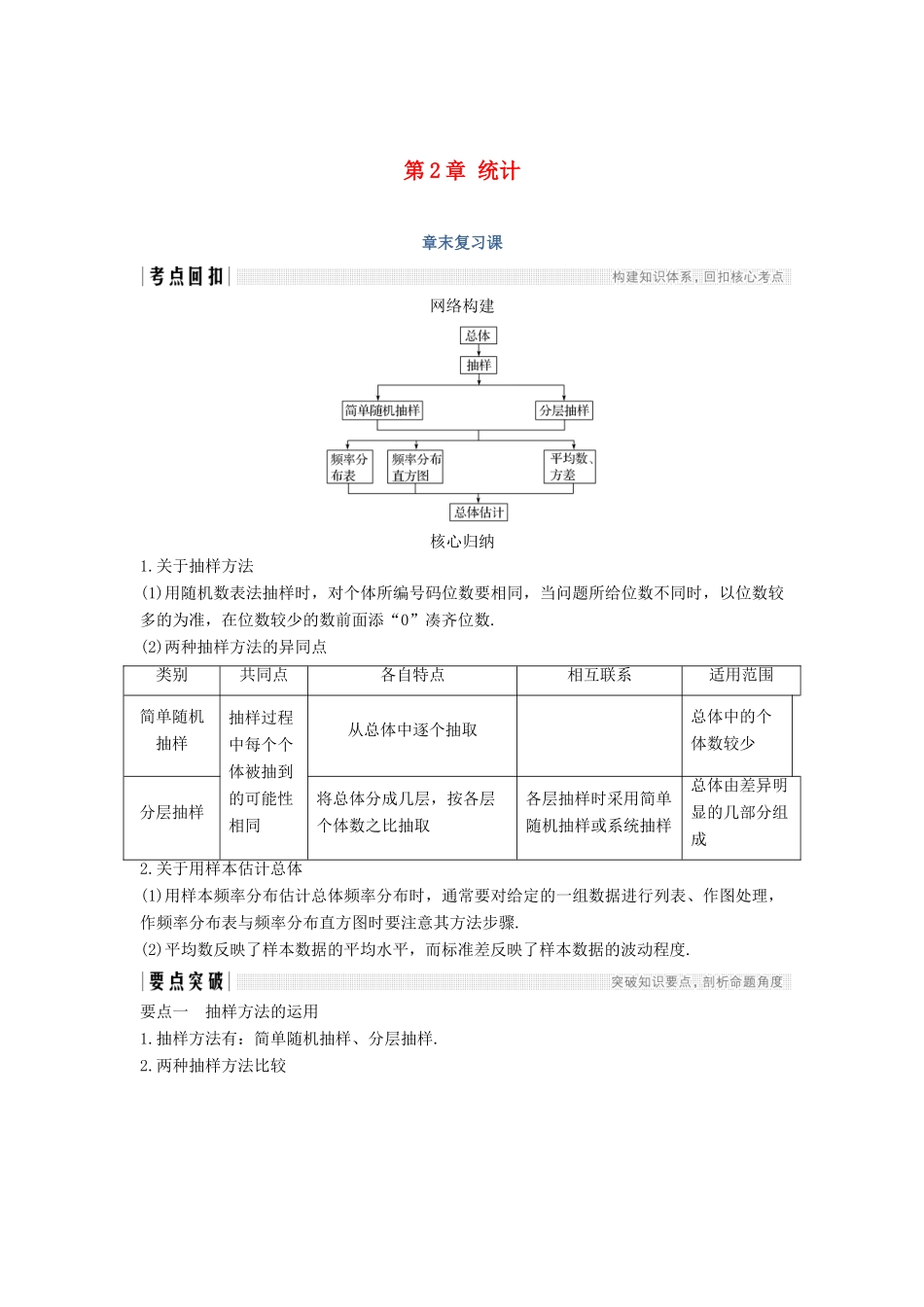
第 2 章 统计章末复习课网络构建核心归纳1.关于抽样方法(1)用随机数表法抽样时,对个体所编号码位数要相同,当问题所给位数不同时,以位数较多的为准,在位数较少的数前面添“0”凑齐位数.(2)两种抽样方法的异同点类别共同点各自特点相互联系适用范围简单随机抽样抽样过程中每个个体被抽到的可能性相同从总体中逐个抽取总体中的个体数较少分层抽样将总体分成几层,按各层个体数之比抽取各层抽样时采用简单随机抽样或系统抽样总体由差异明显的几部分组成2.关于用样本估计总体(1)用样本频率分布估计总体频率分布时,通常要对给定的一组数据进行列表、作图处理,作频率分布表与频率分布直方图时要注意其方法步骤.(2)平均数反映了样本数据的平均水平,而标准差反映了样本数据的波动程度.要点一 抽样方法的运用1.抽样方法有:简单随机抽样、分层抽样.2.两种抽样方法比较【例 1】 某校高一年级有学生 400 人,高二年级有学生 360 人,现采用分层抽样的方法从全校学生中抽出 55 人,其中从高一年级学生中抽出 20 人,则从高三年级学生中抽取的人数为________.解析 由从高一年级学生中抽出 20 人知抽样比为=,所以从高二年级学生中抽取的人数为 360×=18,所以从高三年级学生中抽取的人数为 55-20-18=17.答案 17【训练 1】 某校数学教研组为了解学生学习数学的情况,采用分层抽样的方法从高一 600人、高二 780 人、高三 n 人中,抽取 35 人进行问卷调查.已知高二被抽取的人数为 13,则n=( )A.660 B.720 C.780 D.800解析 由已知条件,抽样比为=,从而=,解得 n=720.答案 B要点二 用样本的频率分布估计总体分布此类问题通常要对样本数据进行列表、作图处理.这类问题采用的图表主要有:条形图、直方图、频率折线图、扇形图等.它们的主要优点是直观,能够清楚表示总体的分布走势.【例 2】 某制造商生产一批直径为 40 mm 的乒乓球,现随机抽样检查 20 个,测得每个球的直径(单位:mm,保留两位小数)如下:40.03 40.00 39.98 40.00 39.99 40.00 39.9840.01 39.98 39.99 40.00 39.99 39.95 40.0140.02 39.98 40.00 39.99 40.00 39.96(1)完成下面的频率分布表,并画出频率分布直方图;分组频数频率[39.95,39.97)[39.97,39.99)[39.99,40.01)[40.01,40.03]合计(2)假定乒乓球的直径误差不超过 0.02 mm 为合格品,若这批乒乓球的总数为10 000 个,试根据抽样检查结果估计这批产品的合格个...