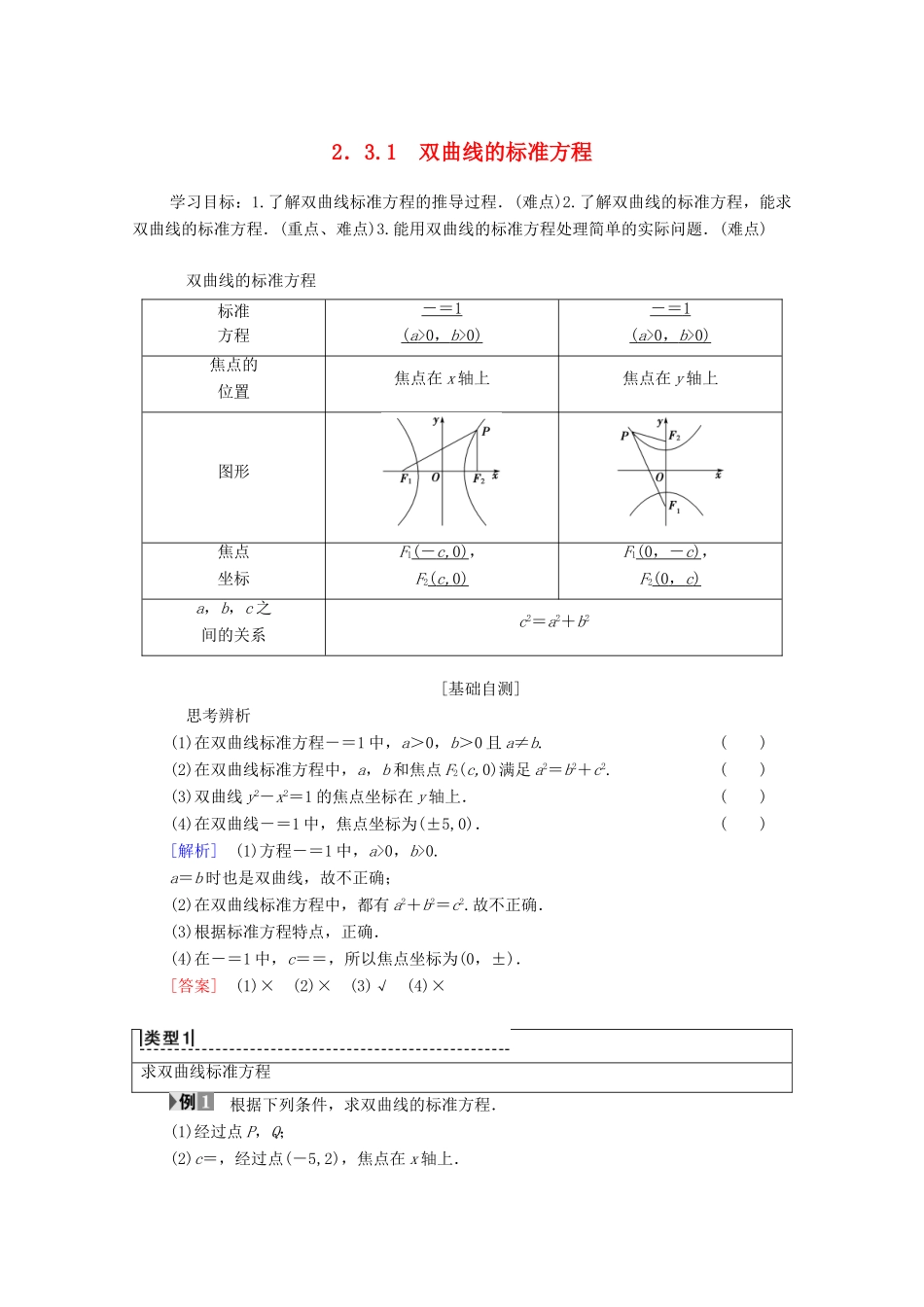
2.3.1 双曲线的标准方程学习目标:1.了解双曲线标准方程的推导过程.(难点)2.了解双曲线的标准方程,能求双曲线的标准方程.(重点、难点)3.能用双曲线的标准方程处理简单的实际问题.(难点) 双曲线的标准方程标准方程-= 1 ( a >0 , b >0) -= 1 ( a >0 , b >0) 焦点的位置焦点在 x 轴上焦点在 y 轴上图形焦点坐标F1( - c, 0) ,F2( c, 0) F1(0 ,- c ) ,F2(0 , c ) a,b,c 之间的关系c2=a2+b2[基础自测] 思考辨析(1)在双曲线标准方程-=1 中,a>0,b>0 且 a≠b.( )(2)在双曲线标准方程中,a,b 和焦点 F2(c,0)满足 a2=b2+c2.( )(3)双曲线 y2-x2=1 的焦点坐标在 y 轴上.( )(4)在双曲线-=1 中,焦点坐标为(±5,0).( )[解析] (1)方程-=1 中,a>0,b>0.a=b 时也是双曲线,故不正确;(2)在双曲线标准方程中,都有 a2+b2=c2.故不正确.(3)根据标准方程特点,正确.(4)在-=1 中,c==,所以焦点坐标为(0,±).[答案] (1)× (2)× (3)√ (4)×求双曲线标准方程 根据下列条件,求双曲线的标准方程.(1)经过点 P,Q;(2)c=,经过点(-5,2),焦点在 x 轴上.[思路探究] 解答(1)可分情况设出双曲线的标准方程,再构造关于 a,b,c 的方程组求解,从而得出双曲线的标准方程.也可以设双曲线方程为 mx2+ny2=1(mn<0)的形式,将两点代入,简化运算过程.解答(2)利用待定系数法.[解] (1)法一:若焦点在 x 轴上,设双曲线的方程为-=1(a>0,b>0),∴点 P 和 Q 在双曲线上,∴解得(舍去)若焦点在 y 轴上,设双曲线的方程为-=1(a>0,b>0),将 P,Q 两点坐标代入可得解得∴双曲线的标准方程为-=1.法二:设双曲线方程为 mx2+ny2=1(mn<0). P,Q 两点在双曲线上,∴解得∴所求双曲线的标准方程为-=1.(2)法一:依题意可设双曲线方程为-=1(a>0,b>0).依题设有解得∴所求双曲线的标准方程为-y2=1.法二: 焦点在 x 轴上,c=,∴设所求双曲线方程为-=1(其中 0<λ<6). 双曲线经过点(-5,2),∴-=1,∴λ=5 或 λ=30(舍去).∴所求双曲线的标准方程是-y2=1.[规律方法] 1.用待定系数法求双曲线方程的一般步骤2.求双曲线标准方程的两个关注点(1)定位:“定位”是指确定与坐标系的相对位置,在“标准方程”的前提下,确定焦点位于哪条坐标轴上,以判断方程的形式;(2)定量:“定量”是指确定 a2,b2的具体数值,常...