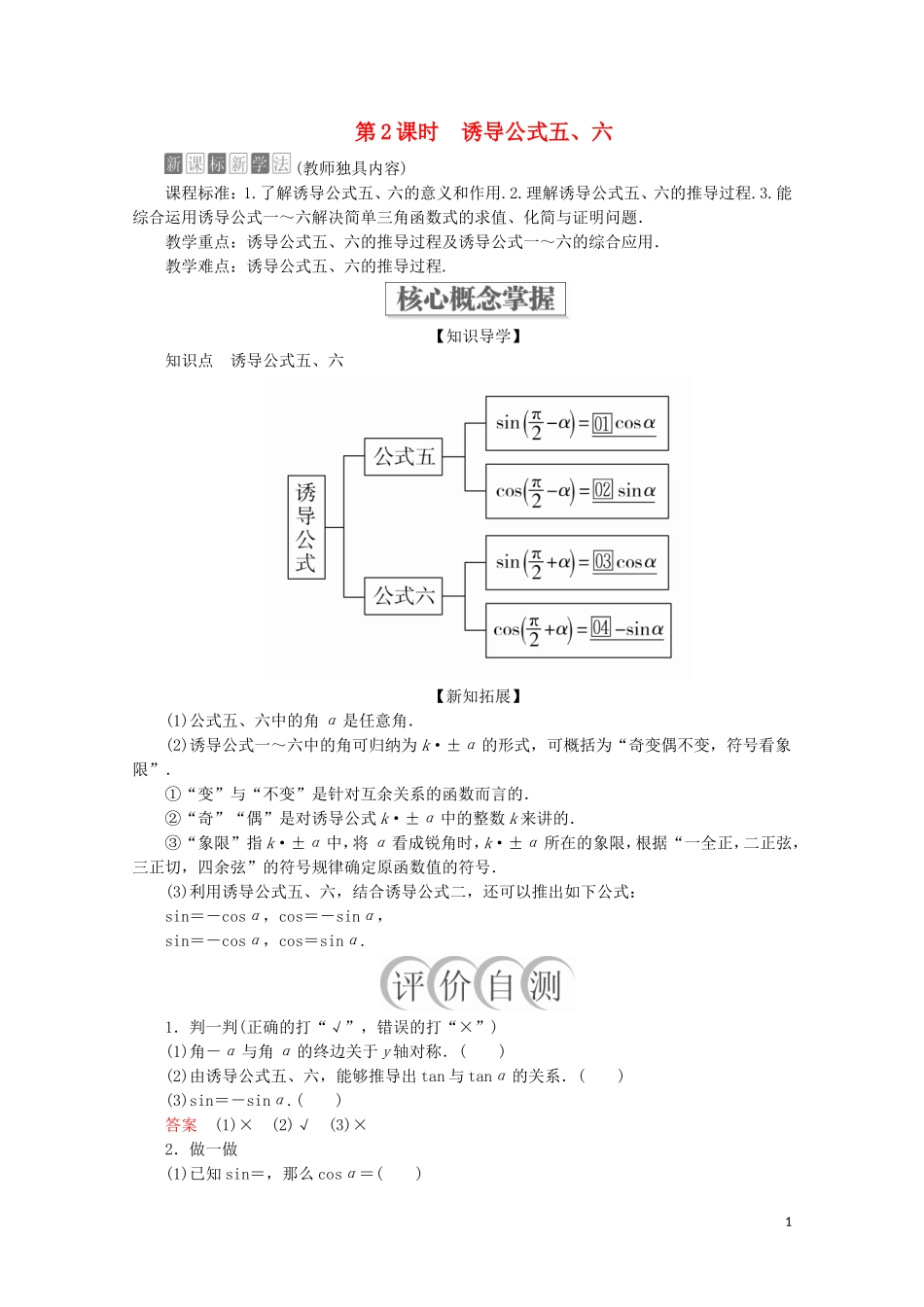
第 2 课时 诱导公式五、六(教师独具内容)课程标准:1.了解诱导公式五、六的意义和作用.2.理解诱导公式五、六的推导过程.3.能综合运用诱导公式一~六解决简单三角函数式的求值、化简与证明问题.教学重点:诱导公式五、六的推导过程及诱导公式一~六的综合应用.教学难点:诱导公式五、六的推导过程.【知识导学】知识点 诱导公式五、六【新知拓展】(1)公式五、六中的角 α 是任意角.(2)诱导公式一~六中的角可归纳为 k·±α 的形式,可概括为“奇变偶不变,符号看象限”.①“变”与“不变”是针对互余关系的函数而言的.②“奇”“偶”是对诱导公式 k·±α 中的整数 k 来讲的.③“象限”指 k·±α 中,将 α 看成锐角时,k·±α 所在的象限,根据“一全正,二正弦,三正切,四余弦”的符号规律确定原函数值的符号.(3)利用诱导公式五、六,结合诱导公式二,还可以推出如下公式:sin=-cosα,cos=-sinα,sin=-cosα,cos=sinα.1.判一判(正确的打“√”,错误的打“×”)(1)角-α 与角 α 的终边关于 y 轴对称.( )(2)由诱导公式五、六,能够推导出 tan 与 tanα 的关系.( )(3)sin=-sinα.( )答案 (1)× (2)√ (3)×2.做一做(1)已知 sin=,那么 cosα=( )1A.- B.- C. D.(2)已知角 α 的终边经过点 P0(-3,-4),则 cos 的值为( )A.- B. C. D.-(3)化简:sin=________.答案 (1)C (2)A (3)-cosα题型一 利用诱导公式五、六求值例 1 已知 cos=,求值:+.[解] 原式=+=-sinα-sinα=-2sinα.又 cos=,所以-sinα=.所以原式=-2sinα=.金版点睛诱导公式应用中需注意的问题诱导公式的应用,就是化归思想的应用,求值过程就是由未知角的三角函数向已知角的三角函数的转化过程.解题时要密切注意角之间的关系,特别是互余、互补关系,为应用诱导公式创造条件. 已知 cos(π+α)=-,求 cos 的值.解 cos(π+α)=-cosα=-,∴cosα=,∴α 为第一或第四象限角.① 若 α 为第一象限角,则 cos=-sinα=-=-=-;② 若 α 为第四象限角,则cos=-sinα===.综上,cos=或-.题型二 化简三角函数式例 2 化简:+.[解] sin=cosα,cos=sinα,cos(π+α)=-cosα,sin(π-α)=sinα,cos=-sinα,sin(π+α)=-sinα,∴原式=+=-sinα+sinα=0.金版点睛2用诱导公式化简求值的方法(1)对于三角函数...