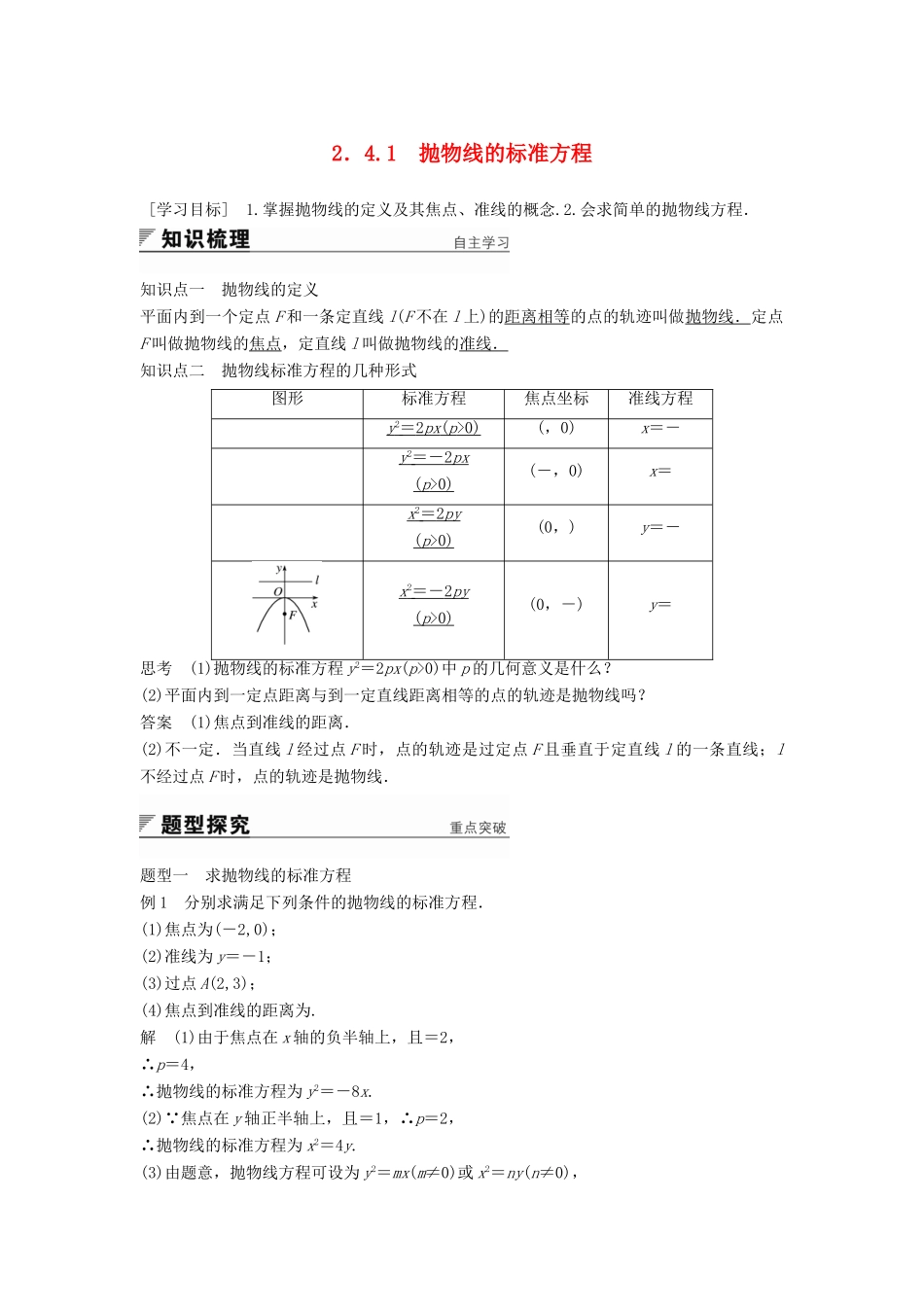
2.4.1 抛物线的标准方程 [学习目标] 1.掌握抛物线的定义及其焦点、准线的概念.2.会求简单的抛物线方程.知识点一 抛物线的定义平面内到一个定点 F 和一条定直线 l(F 不在 l 上)的距离相等的点的轨迹叫做抛物线.定点F 叫做抛物线的焦点,定直线 l 叫做抛物线的准线.知识点二 抛物线标准方程的几种形式图形标准方程焦点坐标准线方程y 2 = 2 px ( p >0) (,0)x=-y 2 =- 2 px ( p >0) (-,0)x=x 2 = 2 py ( p >0) (0,)y=-x 2 =- 2 py ( p >0) (0,-)y=思考 (1)抛物线的标准方程 y2=2px(p>0)中 p 的几何意义是什么?(2)平面内到一定点距离与到一定直线距离相等的点的轨迹是抛物线吗?答案 (1)焦点到准线的距离.(2)不一定.当直线 l 经过点 F 时,点的轨迹是过定点 F 且垂直于定直线 l 的一条直线;l不经过点 F 时,点的轨迹是抛物线.题型一 求抛物线的标准方程例 1 分别求满足下列条件的抛物线的标准方程.(1)焦点为(-2,0);(2)准线为 y=-1;(3)过点 A(2,3);(4)焦点到准线的距离为.解 (1)由于焦点在 x 轴的负半轴上,且=2,∴p=4,∴抛物线的标准方程为 y2=-8x.(2) 焦点在 y 轴正半轴上,且=1,∴p=2,∴抛物线的标准方程为 x2=4y.(3)由题意,抛物线方程可设为 y2=mx(m≠0)或 x2=ny(n≠0),将点 A(2,3)的坐标代入,得 32=m·2 或 22=n·3,∴m=或 n=.∴所求抛物线的标准方程为 y2=x 或 x2=y.(4)由焦点到准线的距离为,可知 p=.∴所求抛物线的标准方程为y2=5x 或 y2=-5x 或 x2=5y 或 x2=-5y.反思与感悟 求抛物线方程,通常用待定系数法,若能确定抛物线的焦点位置,则可设出抛物线的标准方程,求出 p 值即可.若抛物线的焦点位置不确定,则要分情况讨论.焦点在 x 轴上的抛物线方程可设为 y2=ax(a≠0),焦点在 y 轴上的抛物线方程可设为 x2=ay(a≠0).跟踪训练 1 分别求满足下列条件的抛物线的标准方程.(1) 过点(3,-4);(2) 焦点在直线 x+3y+15=0 上.解 (1)方法一 点(3,-4)在第四象限,∴设抛物线的标准方程为 y2=2px (p>0)或 x2=-2p1y (p1>0).把点(3,-4)的坐标分别代入 y2=2px 和 x2=-2p1y,得(-4)2=2p·3,32=-2p1·(-4),即 2p=,2p1=.∴所求抛物线的标准方程为 y2=x 或 x2=-y.方法二 点(3,-4)在第四象限,∴抛物线的方程可设为 y2=...