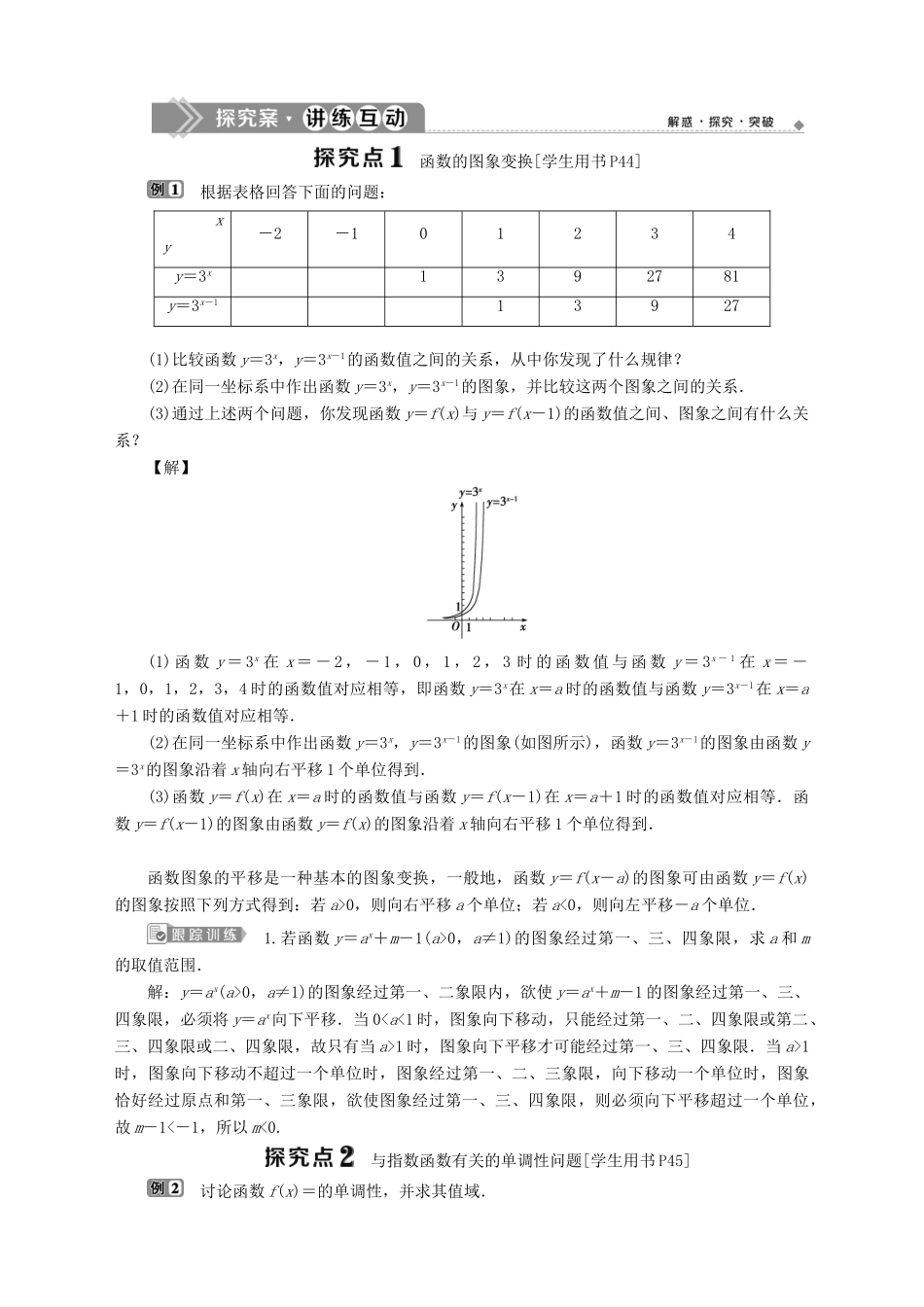
第 2 课时 指数函数及其性质的应用 1.了解指数函数模型解决简单的实际问题. 2.理解图象的平移变换、对称变换.3.掌握指数函数图象与性质的应用. [学生用书 P44]与作函数图象相关的几种常见的变换(1)平移变换① 沿 x 轴:将 y=f(x)的图象向左(a>0)或向右(a<0)平移|a|个单位以后,得到函数 y=f(x+a),(a≠0)的图象;② 沿 y 轴:将 y=f(x)的图象向上(b>0)或向下(b<0)平移|b|个单位以后,得到函数 y=f(x)+b,(b≠0)的图象.(2)对称变换①y=f(-x)的图象与 y=f(x)的图象关于 y 轴对称;②y=-f(x)的图象与 y=f(x)的图象关于 x 轴对称;③y=-f(-x)的图象与 y=f(x)的图象关于原点(0,0)对称;④y=f(a+x)的图象与 y=f(b-x)的图象关于直线 x=对称.⑤y=f(|x|)是偶函数,图象关于 y 轴对称,x≥0 时与 y=f(x)图象重合,所以 x<0 时的图象与 x≥0 时 y=f(x)的图象关于 y 轴对称;⑥y=|f(x)|=y=|f(x)|的图象是 y=f(x)(f(x)≥0)与 y=-f(x)(f(x)<0)图象的组合.1.已知指数函数 f(x)的图象过点,则 f(-3)=________.解析:设 f(x)=ax(a>0,且 a≠1),则 a4=,所以 a=.所以 f(x)=.所以 f(-3)==8.答案:82.函数 y=ax-3+3(a>0,且 a≠1)的图象恒过定点________. 解析:因为函数 y=ax(a>0,且 a≠1)过定点(0,1),函数 y=ax-3+3 中,令 x=3,得 y=1+3=4,所以函数的图象过定点(3,4).答案:(3,4)3.已知 0<a<1,b<-1,则函数 y=ax+b 的图象必定不经过第________象限.解析:过点(0,1+b),因为 b<-1,所以点(0,1+b)在 y 轴负半轴上.故图象不经过第一象限.答案:一4.函数 y=2x+1的图象是________.解析:当 x=0 时,y=2,且函数单调递增.答案:① 函数的图象变换[学生用书 P44] 根据表格回答下面的问题:xy -2-101234y=3x1392781y=3x-113927(1)比较函数 y=3x,y=3x-1的函数值之间的关系,从中你发现了什么规律?(2)在同一坐标系中作出函数 y=3x,y=3x-1的图象,并比较这两个图象之间的关系.(3)通过上述两个问题,你发现函数 y=f(x)与 y=f(x-1)的函数值之间、图象之间有什么关系?【解】 (1) 函 数 y = 3x 在 x = - 2 , - 1 , 0 , 1 , 2 , 3 时 的 函 数 值 与 函 数 y = 3x - 1 在 x = -1,0,1,2,3,4 时的函数值对应相等,即函数 ...