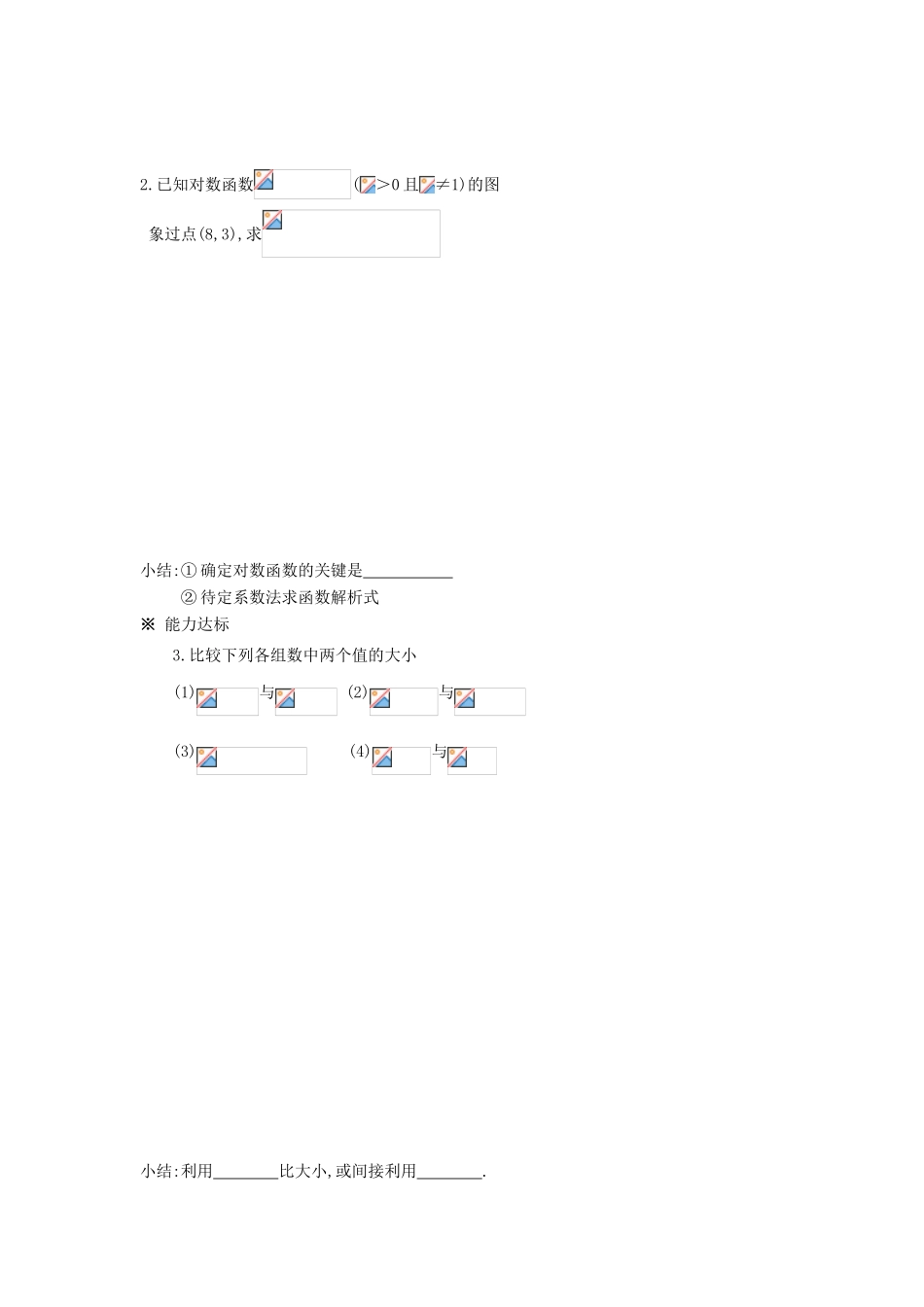
§2.2.2 对数函数及其性质(一)学习目标 1.了解对数函数模型的实际背景,认识数学与现实 生活及其他学科的联系2.理解对数函数的概念3.能画出具体对数函数的图象,掌握对数函数的图 象、性质※ 学习重点、难点:重点:对数函数的图象、性质难点:对数函数的图象、性质与底数 a 的关系,如何 由图像,解析式归纳对数函数的性质学习过程 (预习教材 P70~ P72,找出疑惑之处)一.课前导学※ 情景引入探究 1:对数函数的概念问题 1:若请同学们计算并填写下表p124t观察体会:对,能否称 t 是关于 p 的函数,为什么?新知:对数函数的概念 一般地,我们把函数 叫做对数函数,其中 是自变量,函数的定义域是 反思:(1)为什么规定>0 且≠1 呢?(2)为什么对数函数 (>0 且≠1)的定义域是(0,+∞)?探究 2:对数函数的图像与性质问题 3:在同一坐标系中画出下列函数图象: y 0 x讨论:(1)函数与 的图象有什么关系 ?如何由的图象画出 的图象?(2)根据对数函数的图象特征,归纳出对数函数的性 质异同?主要与什么有关? 新知:对数函数的性质二.课内探究※ 知识检测1.下列函数中,哪些是对数函数?(1)(且) (2)(3)(4)(且) (5)(6)小结:判断对数函数的方法: x… 124……………0<a<1a>1图象性质定义域: 值域: 过点 ,即 x= 时,y= 在(0,+∞)上是 在(0,+∞)上是 2.已知对数函数(>0 且≠1)的图 象过点(8,3),求小结:① 确定对数函数的关键是 ② 待定系数法求函数解析式※ 能力达标3.比较下列各组数中两个值的大小(1)与 (2)与 (3) (4)与小结:利用 比大小,或间接利用 .4.已知下列不等式,比较正数 m、n 的大小:(1)m<n (2)m>n (3)m<n(0<a<1) (4)m>n(a>1)※ 拓展提高5.比较大小:与小结:三.总结提升※ 学习小结1.对数函数的概念2.对数函数的图象与性质3.比较对数大小的方法四.课后作业1.对数函数的图象过点,则此对数函数的解析式为 ( )A. B.C. D.2.当 a>1 时,在同一坐标系中,函数与 的图象是( )3.已知函数,则 4.比较大小 (1), (2), (3)log 89,log 98 (4)log 31.5,log 2 0.8