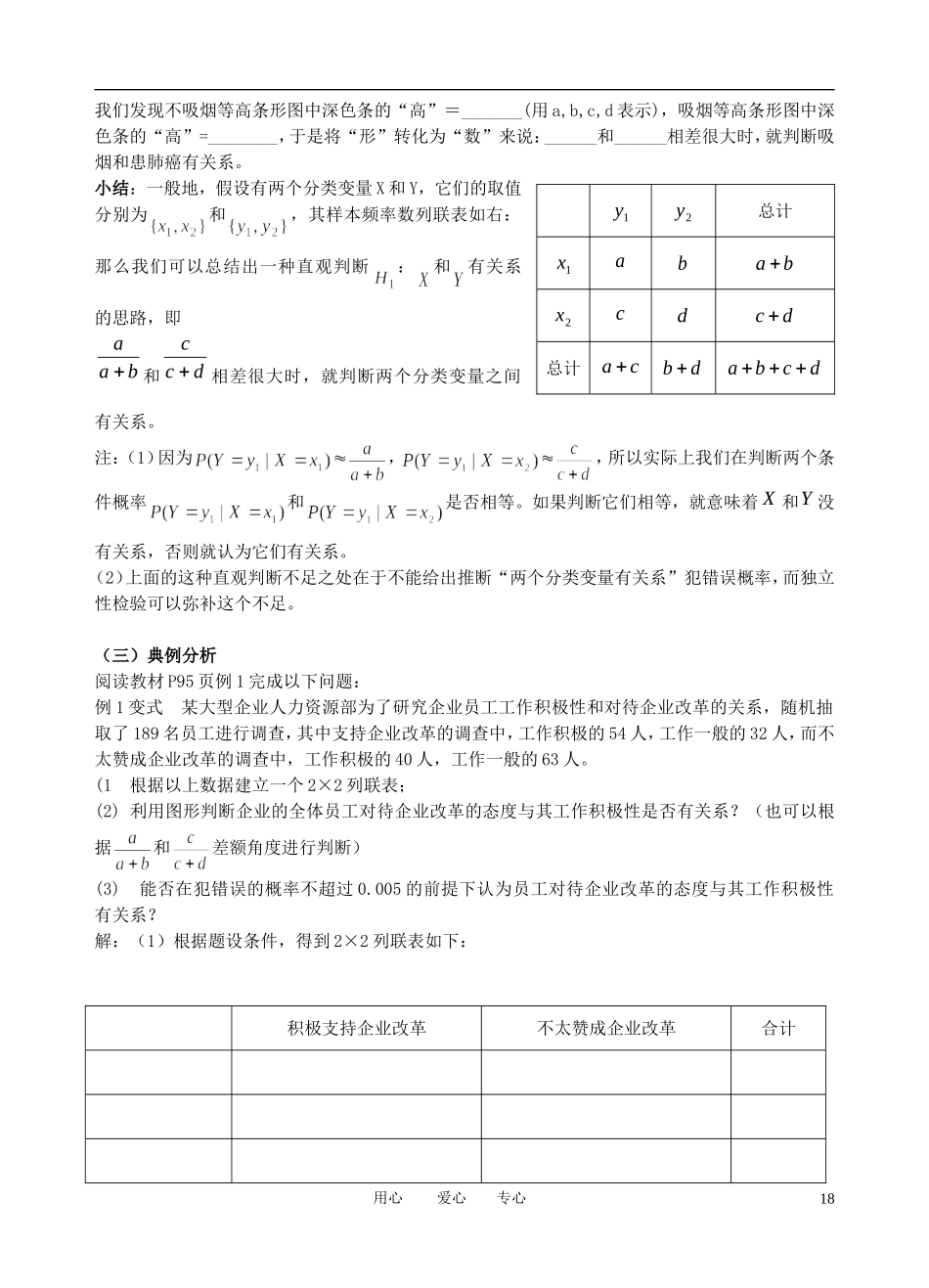
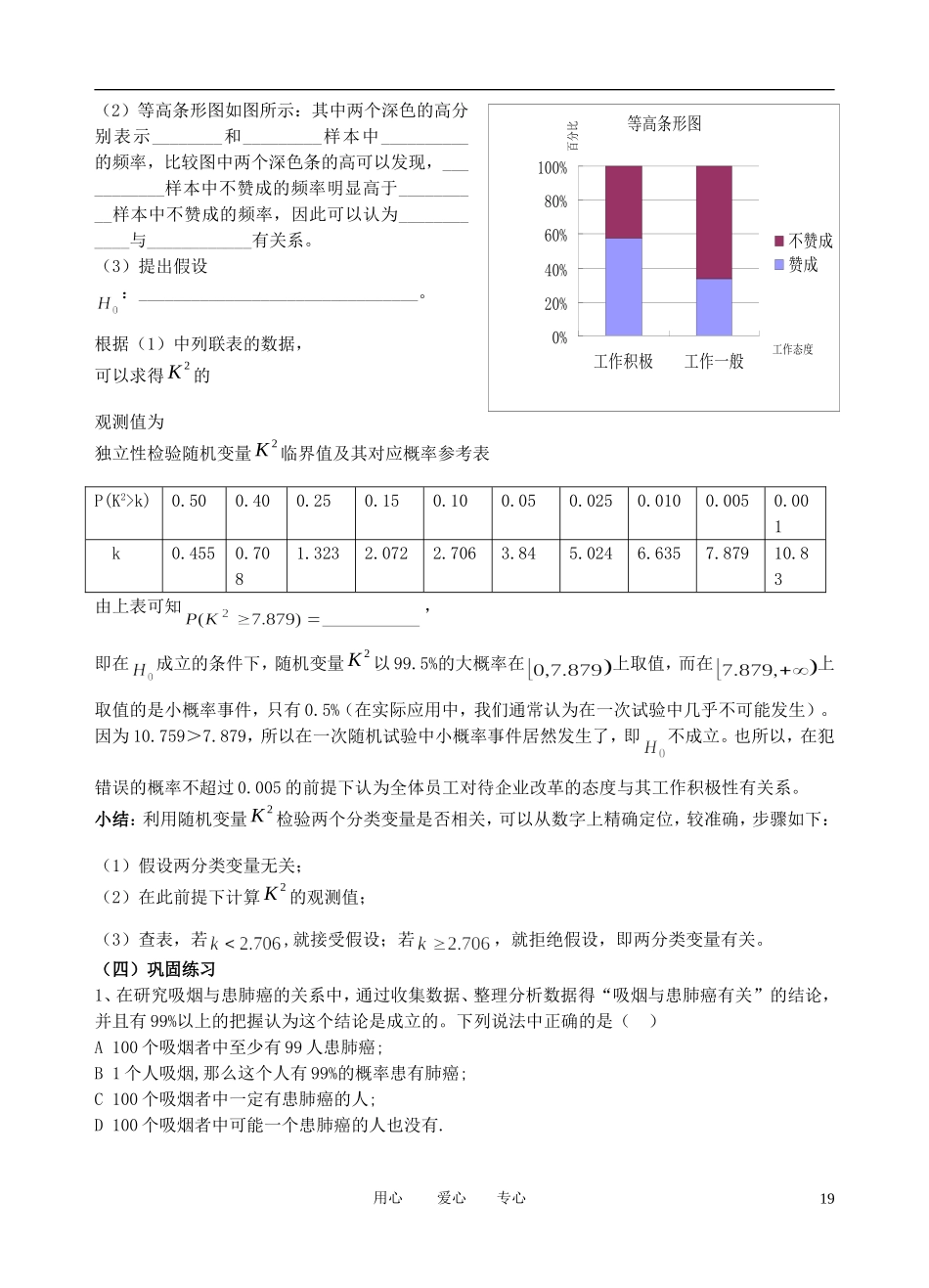
0%20%40%60%80%100%不吸烟吸 烟患肺癌不患肺癌第 44 课时 独立性检验的基本思想及其初步应用(二)学习目标:1、进一步掌握的计算公式及它的实际意义,掌握计算这种判断的可靠程度的具体做法.2、加强与现实生活相联系,学会用数据来准确描述两个变量的关系,明确数学在现实生活中的重要作用和实际价值。教学重点;独立性检验的基本思想、实施步聚教学难点:独立性检验的基本思想、随机变量的含义教学工具:Powerpoint、Excel教学过程:(一) 复习引入1、独立性检验:这种利用随机变量来确定是否能以给定把握认为“两个分类变量有关系”的方法。2、独立性检验的步聚第一步:提出假设检验问题:吸烟与患肺癌没有关系:吸烟与患肺癌有关系;第二步:选择检验的指标(它越小,原假设“H :吸烟与患肺癌没有关系”成立的可能性越大;它越大,备择假设“H :吸烟与患肺癌有关系”成立的可能性越大;第三步:查临界值表得出结论.P(k2>k)0.500.400.250.150.100.050.0250.0100.0050.001 k0.4550.7081.3232.0722.7063.845.0246.6357.87910.83(二) 推进新课阅读教材 P94页-P96页材料:下面是吸烟与患肺癌的 2×2 列联表,其等高条形图如下:在等高条形图中,深色条的高分别表示不吸烟和吸烟样本中患肺癌的频率.从等高条形图中我们直观上认为吸烟更容易引发肺癌.更进一步有(列联表中数字用字母代替)不患肺癌患肺癌总计不吸烟abab吸 烟cdcd总 计acbdabcd 用心 爱心 专心不患肺癌患肺癌总计不吸烟 7775 427817吸 烟 2099 492148总 计 9874 91996517我们发现不吸烟等高条形图中深色条的“高”=_______(用 a,b,c,d 表示),吸烟等高条形图中深色条的“高”=________,于是将“形”转化为“数”来说:______和______相差很大时,就判断吸烟和患肺癌有关系。小结:一般地,假设有两个分类变量 X 和 Y,它们的取值分别为和,其样本频率数列联表如右:那么我们可以总结出一种直观判断:和有关系的思路,即baa和dcc相差很大时,就判断两个分类变量之间有关系。注:(1)因为,,所以实际上我们在判断两个条件概率和是否相等。如果判断它们相等,就意味着 X 和Y 没有关系,否则就认为它们有关系。(2)上面的这种直观判断不足之处在于不能给出推断“两个分类变量有关系”犯错误概率,而独立性检验可以弥补这个不足。(三)典例分析阅读教材 P95 页例 1 完成以下问题:例 1 变式 某大型企业人力资源部为了...