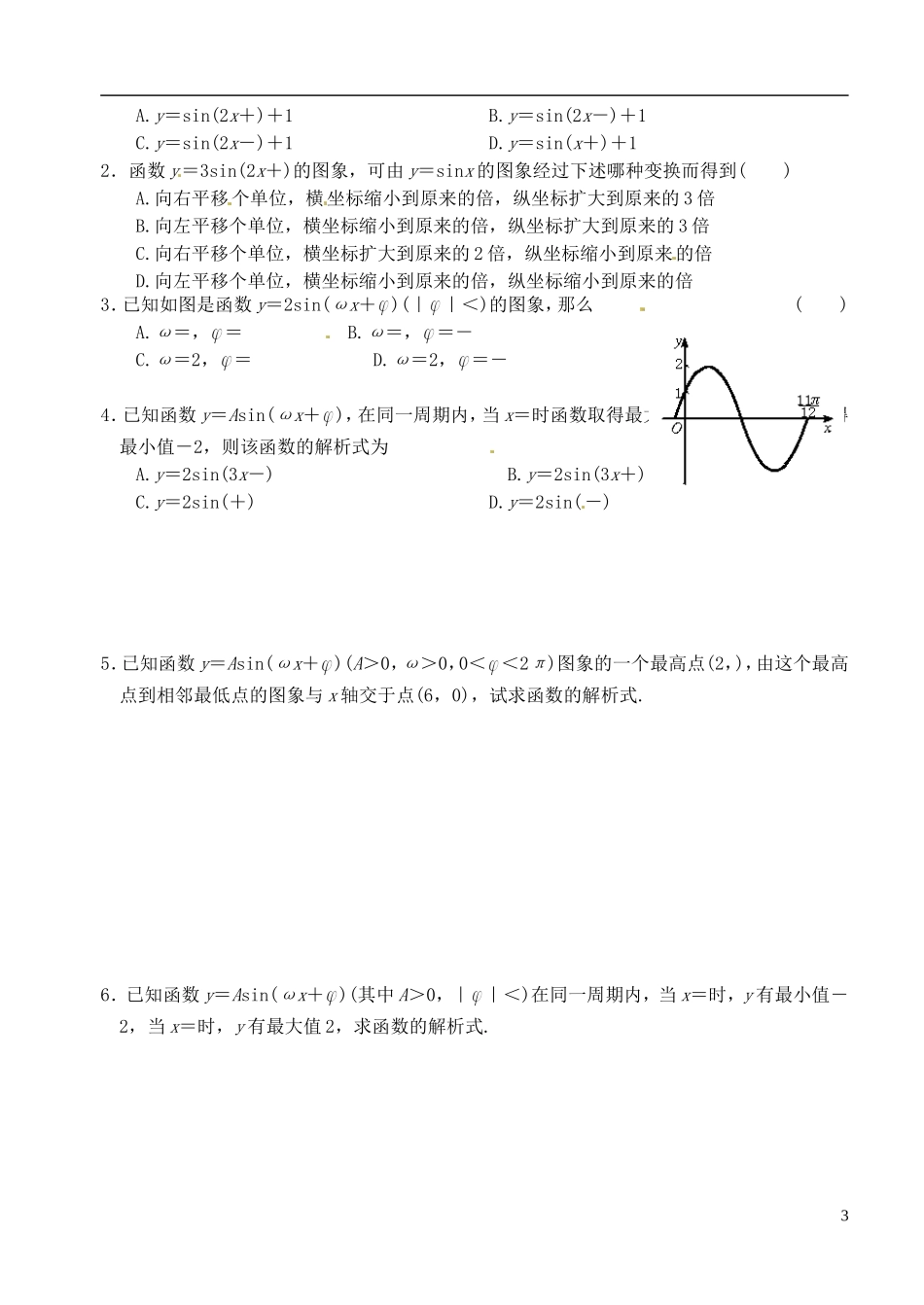
第十八课时 函数 y=Asin(ωx+ )的图象(三)教学目标:会用“五点法”画 y=Asin(ωx+ )的图象,会用图象变换的方法画 y=Asin(ωx+ )的图象,会求一些函数的振幅、周期、最值等;数形结合思想的渗透,化归思想的渗透,提高数学素质.教学重点:1.“五点法”画 y=Asin(ωx+ )的图象;2.图象变换过程的理解;3.一些相关概念.教学难点:多种变换的顺序教学过程:Ⅰ.课题导入y=A sin(ωx+ )(其中 A>0,ω>0, ≠0)的图象又该如何得到?[例]画出函数 y=3sin(2x+),x∈R 的简图.解:(五点法)列表:x2x+3sin(2x+)描点画图:这种曲线也可由图象变换得到:一般地,函数 y=Asin(ωx+ ),x∈R(其中 A>0,ω>0)的图象,可以看作用下面的方法得到:先把正弦曲线上所有的点向 (当 >0 时)或向 (当 <0 时)平行移动 个单位1长度,再把所得各点的横坐标 (当 ω>1 时)或 (当 0<ω<1 时)到原来的 倍(纵坐标不变),再把所得各点的纵坐标 (当 A>1 时)或 (当 0<A<1 时)到原来的 倍(横坐标不变).注意一些物理量的概念:A 称为 T= 称为 f= 称为 ωx+ 称为 x=0 时的相位 称为 Ⅲ.课堂练习课本 P42 1~6Ⅳ.课时小结Ⅴ.课后作业课本 P46 8函数 y=Asin(ωx+ )的图象(三)1.若函数y=f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的 2 倍,然后再将整个图象沿 x 轴向左平移 个单位,沿 y 轴向下平移 1 个单位,得到函数 y=sinx 的图象,则有y=f(x)是 ( )2A.y=sin(2x+)+1 B.y=sin(2x-)+1C.y=sin(2x-)+1 D.y=sin(x+)+12.函数 y=3sin(2x+)的图象,可由 y=sinx 的图象经过下述哪种变换而得到( )A.向右平移个单位,横坐标缩小到原来的倍,纵坐标扩大到原来的 3 倍B.向左平移个单位,横坐标缩小到原来的倍,纵坐标扩大到原来的 3 倍C.向右平移个单位,横坐标扩大到原来的 2 倍,纵坐标缩小到原来的倍D.向左平移个单位,横坐标缩小到原来的倍,纵坐标缩小到原来的倍3.已知如图是函数 y=2sin(ωx+ )(| |<)的图象,那么 ( )A.ω=, = B.ω=, =- C.ω=2, = D.ω=2, =-4.已知函数 y=Asin(ωx+ ),在同一周期内,当 x=时函数取得最大值 2,当 x=时函数取得最小值-2,则该函数的解析式为 ( )A.y=2sin(3x-) B.y=2sin(3x+)C.y=2sin(+) D.y=2sin(-)5.已知函数 y=Asin(ωx+ )(A>0,ω...