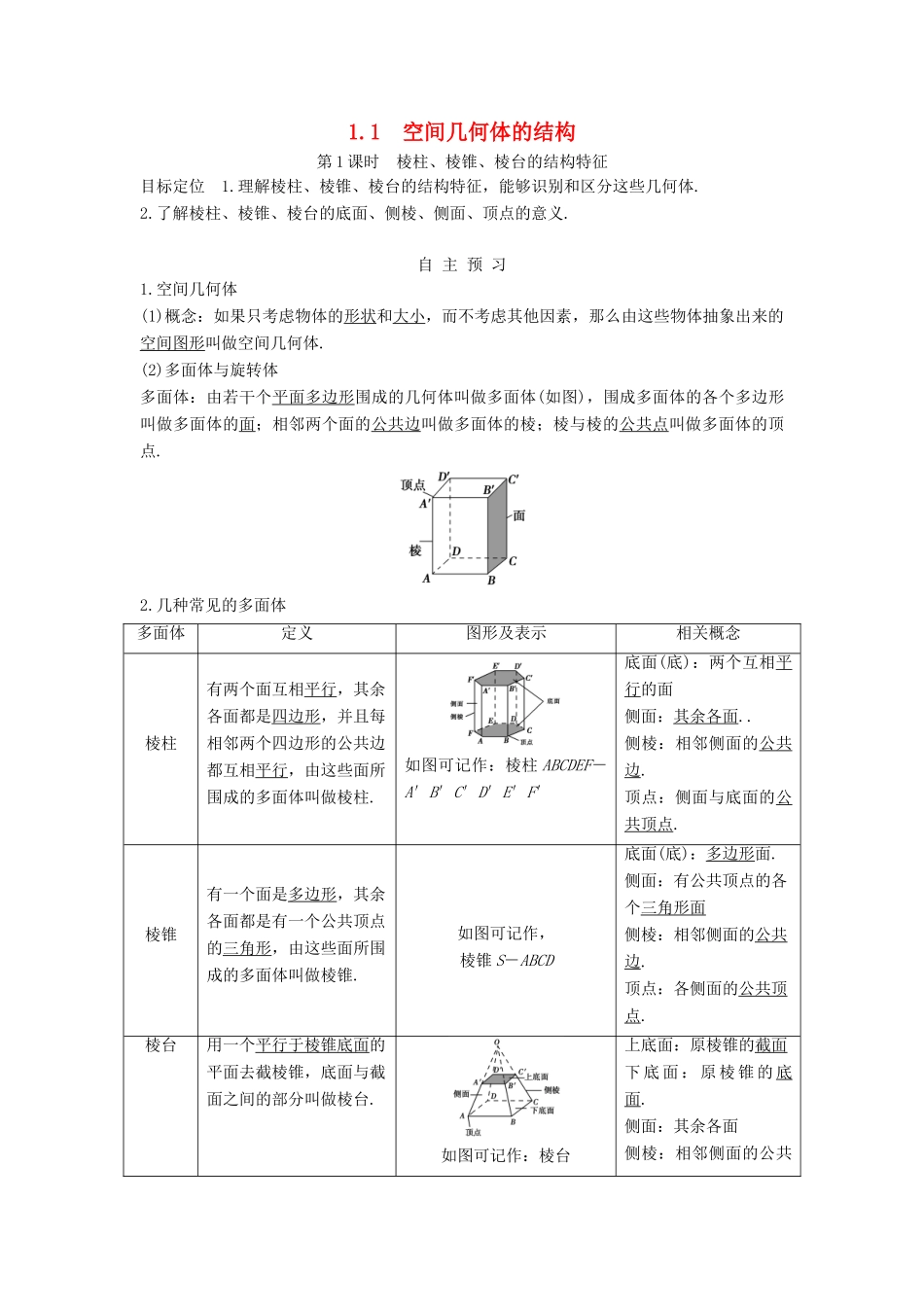
1.1 空间几何体的结构第 1 课时 棱柱、棱锥、棱台的结构特征目标定位 1.理解棱柱、棱锥、棱台的结构特征,能够识别和区分这些几何体.2.了解棱柱、棱锥、棱台的底面、侧棱、侧面、顶点的意义.自 主 预 习1.空间几何体(1)概念:如果只考虑物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形叫做空间几何体.(2)多面体与旋转体多面体:由若干个平面多边形围成的几何体叫做多面体(如图),围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点.2.几种常见的多面体多面体定义图形及表示相关概念棱柱有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱.如图可记作:棱柱 ABCDEF-A′B′C′D′E′F′底面(底):两个互相平行的面侧面:其余各面..侧棱:相邻侧面的公共边.顶点:侧面与底面的公共顶点.棱锥有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥.如图可记作,棱锥 S-ABCD底面(底):多边形面.侧面:有公共顶点的各个三角形面侧棱:相邻侧面的公共边.顶点:各侧面的公共顶点.棱台用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫做棱台.如图可记作:棱台上底面:原棱锥的截面下 底 面 : 原 棱 锥 的 底面.侧面:其余各面侧棱:相邻侧面的公共ABCD-A′B′C′D′边.顶点:侧面与上(下)底面的公共顶点.即 时 自 测1.判断题(1)棱柱的侧棱长相等,侧面是平行四边形.(√)(2)各侧面都是正方形的四棱柱一定是正方体.(×)(3)正棱锥的侧面是等边三角形.(×)(4)用一个平面去截棱锥;棱锥底面和截面之间的部分是棱台.(×)提示 (1)由棱柱定义可知,棱柱的侧棱相互平行且相等,所以侧面均为平行四边形.(2)上、下底面是菱形,各侧面是全等的正方形的四棱柱不一定是正方体.(3)正棱锥的侧面都是等腰三角形,不一定是等边三角形.(4)该平面不一定平行于底面.2.下列说法中正确的是( )A.棱柱仅有一个底面 B.棱柱的顶点至少有 6 个C.棱柱的侧棱至少有 4 条 D.棱柱的棱至少有 4 条答案 B3.下列棱锥有 6 个面的是( )A.三棱锥 B.四棱锥 C.五棱锥 D.六棱锥答案 C4.一个棱柱至少有________个面,面数最少的一个棱锥有________个面,顶点最少的一个棱台有________条侧棱.解析 面数最少的棱柱为三棱柱,有 5 个面;面数最少的棱锥为三棱锥...