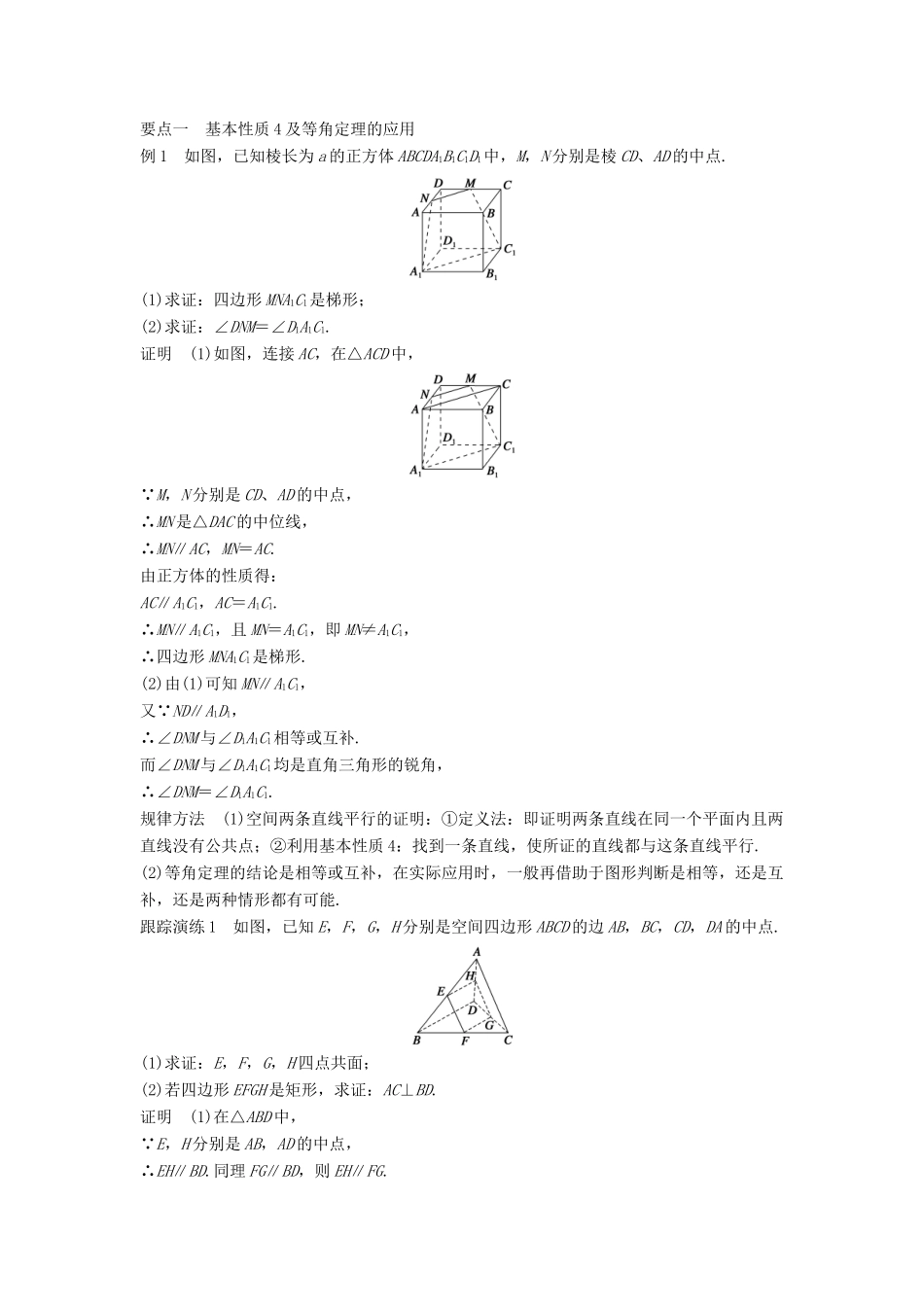
1.2.2 第 1 课时 平行直线、直线与平面平行[学习目标] 1.能认识和理解空间平行线的传递性,会证明空间等角定理.2.掌握直线与平面平行的判定定理和性质定理,并能利用两个定理解决空间中的平行关系问题.[知识链接]1.直线和平面的位置关系有:平行、相交、直线在平面内 . 2.当直线与平面无公共点时,直线和平面平行.[预习导引]1.平行直线的定义及平行公理在平面几何中,我们把在同一个平面内不相交的两条直线叫做平行线.平行公理:过直线外一点有且只有一条直线和已知直线平行.2.基本性质 4平行于同一条直线的两条直线互相平行,即如果直线 a∥b,c∥b,那么 a ∥ c .3.等角定理如果一个角的两边与另一个角的两边分别对应平行,并且方向相同,那么这两个角相等.解决学生凝难点: 4.直线和平面的位置关系位置关系直线 a 在平面 α 内直线 a 与平面 α 相交直线 a 与平面 α 平行公共点有无数个公共点有且只有一个公共点没有公共点符号表示a ⊂ α a ∩ α = A a ∥ α 图形表示5.直线与平面平行的判定定理及性质定理定理条件结论符号语言判定如果不在一个平面内的一条直线和平面内的一条直线平行 这条直线和这个平面平行l ⊄ α ,m⊂α,l ∥ m ⇒l ∥ α 性质如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交这条直线和这两个平面的交线平行l∥α,l ⊂ β ,α ∩ β =m⇒l∥m要点一 基本性质 4 及等角定理的应用例 1 如图,已知棱长为 a 的正方体 ABCDA1B1C1D1中,M,N 分别是棱 CD、AD 的中点.(1)求证:四边形 MNA1C1是梯形;(2)求证:∠DNM=∠D1A1C1.证明 (1)如图,连接 AC,在△ACD 中, M,N 分别是 CD、AD 的中点,∴MN 是△DAC 的中位线,∴MN∥AC,MN=AC.由正方体的性质得:AC∥A1C1,AC=A1C1.∴MN∥A1C1,且 MN=A1C1,即 MN≠A1C1,∴四边形 MNA1C1是梯形.(2)由(1)可知 MN∥A1C1,又 ND∥A1D1,∴∠DNM 与∠D1A1C1相等或互补.而∠DNM 与∠D1A1C1均是直角三角形的锐角,∴∠DNM=∠D1A1C1.规律方法 (1)空间两条直线平行的证明:①定义法:即证明两条直线在同一个平面内且两直线没有公共点;②利用基本性质 4:找到一条直线,使所证的直线都与这条直线平行.(2)等角定理的结论是相等或互补,在实际应用时,一般再借助于图形判断是相等,还是互补,还是两种情形都有可能.跟踪演练 1 如图,已知 E,F,G,H 分别是空间四边形 AB...