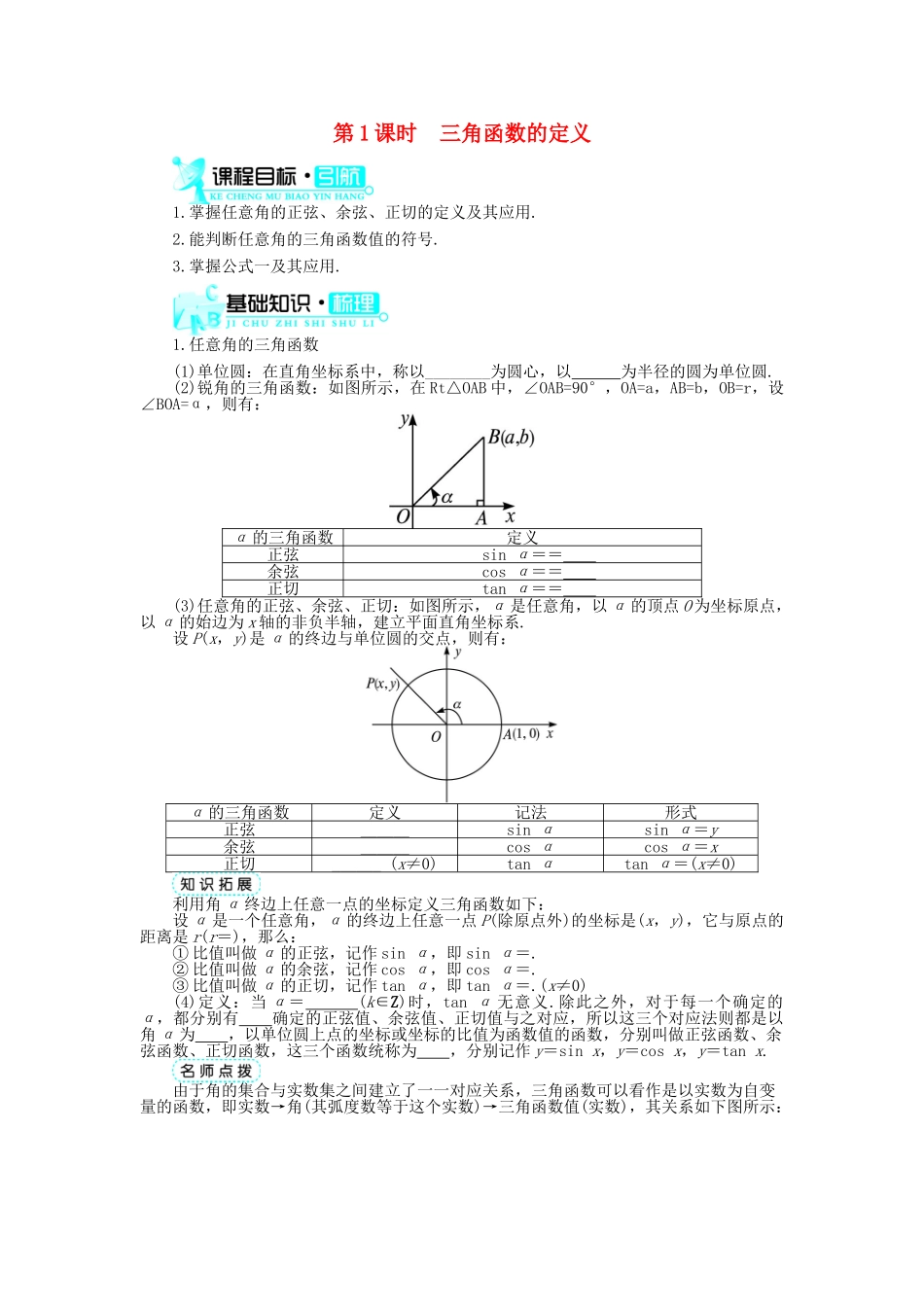
第 1 课时 三角函数的定义1.掌握任意角的正弦、余弦、正切的定义及其应用.2.能判断任意角的三角函数值的符号.3.掌握公式一及其应用.1.任意角的三角函数(1)单位圆:在直角坐标系中,称以________为圆心,以 为半径的圆为单位圆.(2)锐角的三角函数:如图所示,在 Rt△OAB 中,∠OAB=90°,OA=a,AB=b,OB=r,设∠BOA=α,则有:α 的三角函数定义正弦sin α== 余弦cos α== 正切tan α== (3)任意角的正弦、余弦、正切:如图所示,α 是任意角,以 α 的顶点 O 为坐标原点,以 α 的始边为 x 轴的非负半轴,建立平面直角坐标系.设 P(x,y)是 α 的终边与单位圆的交点,则有:α 的三角函数定义记法形式正弦______sin αsin α=y余弦______cos αcos α=x正切______ (x≠0)tan αtan α=(x≠0)利用角 α 终边上任意一点的坐标定义三角函数如下:设 α 是一个任意角,α 的终边上任意一点 P(除原点外)的坐标是(x,y),它与原点的距离是 r(r=),那么:① 比值叫做 α 的正弦,记作 sin α,即 sin α=.② 比值叫做 α 的余弦,记作 cos α,即 cos α=.③ 比值叫做 α 的正切,记作 tan α,即 tan α=.(x≠0)(4)定义:当 α= (k∈Z)时,tan α 无意义.除此之外,对于每一个确定的α,都分别有 确定的正弦值、余弦值、正切值与之对应,所以这三个对应法则都是以角 α 为 ,以单位圆上点的坐标或坐标的比值为函数值的函数,分别叫做正弦函数、余弦函数、正切函数,这三个函数统称为 ,分别记作 y=sin x,y=cos x,y=tan x.由于角的集合与实数集之间建立了一一对应关系,三角函数可以看作是以实数为自变量的函数,即实数→角(其弧度数等于这个实数)→三角函数值(实数),其关系如下图所示:(5)定义域:如表所示,三角函数解析式定义域正弦函数y=sin x_______余弦函数y=cos x____正切函数y=tan x_______【做一做 1-1】 若角 α 终边上有一点 P(0,3),则下列式子无意义的是( )A.tan αB.sin αC.cos α D.sin αcos α【做一做 1-2】 若角 α 的终边与单位圆相交于点,则 sin α 的值为( )A. B.- C. D.-12.三角函数值的符号sin α,cos α,tan α 在各个象限的符号如下:正弦、余弦和正切函数在各象限的符号可用以下口诀记忆:“一全正,二正弦,三正切,四余弦”.其含义是在第一象限各三角函数值全为正,在第二象限只有...