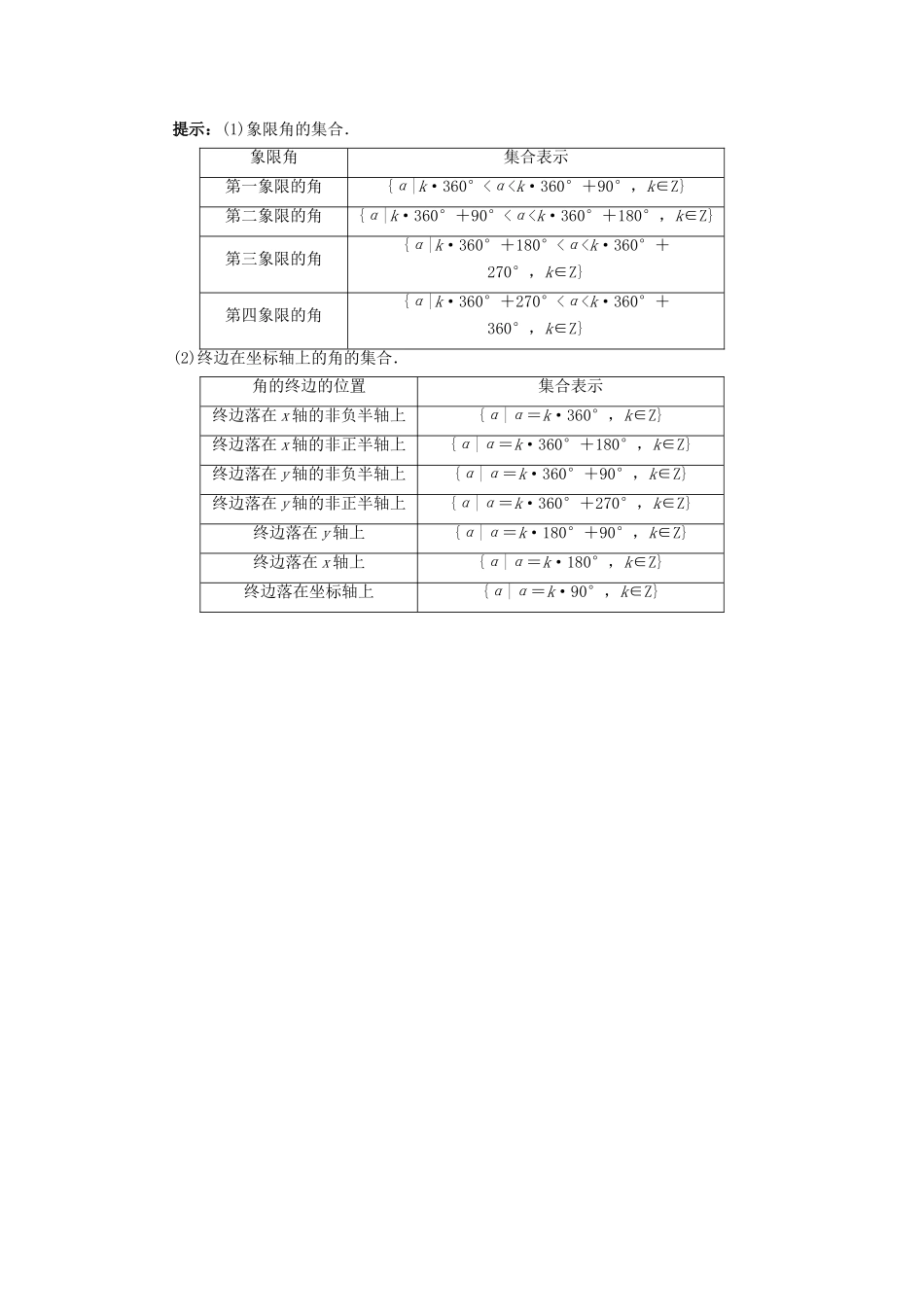
1.1.1 角的概念的推广预习导航课程目标学习脉络1.理解任意角的概念,注意任意角的三个要素:顶点、始边、终边.用旋转的观点来定义角,抓住:(1)旋转方向;(2)旋转大小.2.理解并掌握终边相同的角,会将角放在坐标系中去体会.3.掌握象限角及轴线角的表示.1.任意角(1)角的定义.① 静态定义:有公共端点的两条射线组成的图形叫做角,这个公共端点叫做角的顶点,这两条射线叫做角的边.② 动态定义:一条射线绕着它的端点从一个位置旋转到另一个位置所成的图形叫做角,旋转射线的端点叫做角的顶点,开始位置的射线叫做角的始边,终止位置的射线叫做角的终边.在画图时,常用带箭头的弧来表示旋转的方向和旋转的绝对量,旋转生成的角,又常叫做转角.(2)角的记法.用一个希腊字母表示;用三个大写的英文字母表示(字母前面要写“∠”).(3)角的分类.任意角定义正角按逆时针方向旋转而成的角负角按顺时针方向旋转而成的角零角一条射线没有作任何旋转而成的角(4)角的运算.引入正角、负角的概念以后,角的减法运算可以转化为角的加法运算,即 α-β 可以化为 α + ( - β ) . 这就是说,各角和的旋转量等于各角旋转量的和.归纳总结(1)掌握角的概念应注意角的三要素:顶点、始边、终边.(2)高中阶段所说的角实际上是初中平面几何中“角是从一点出发的两条射线所组成的图形”的概念的推广,这里重点强调“角是由一条射线绕着它的端点旋转而成的”这一运动的观点.(3)角不仅有大小而且有正负,角的概念的推广重在“旋转”两字.其旋转方向决定了角的正负,由此确定了角的分类.2.终边相同的角设 α 表示任意角,所有与 α 终边相同的角,包括 α 本身构成一个集合,这个集合可记为 S={β|β=α+k·360°,k∈Z},即任一与角 α 终边相同的角,都可以表示成角α 与整数个周角的和的形式.归纳总结 (1)α 为任意角.(2)k·360°-α,k∈Z 可理解为 k·360°+(-α),k∈Z.(3)相等的角终边一定相同,终边相同的角不一定相等,终边相同的角有无数个,它们相差 360°的整数倍.(4)k∈Z 这一条件不可少.(5)零角的始边和终边相同,但始边和终边相同的角并不一定是零角.自主思考 1 已知介于两个角之间的角的集合叫做区间角,如{x|60°