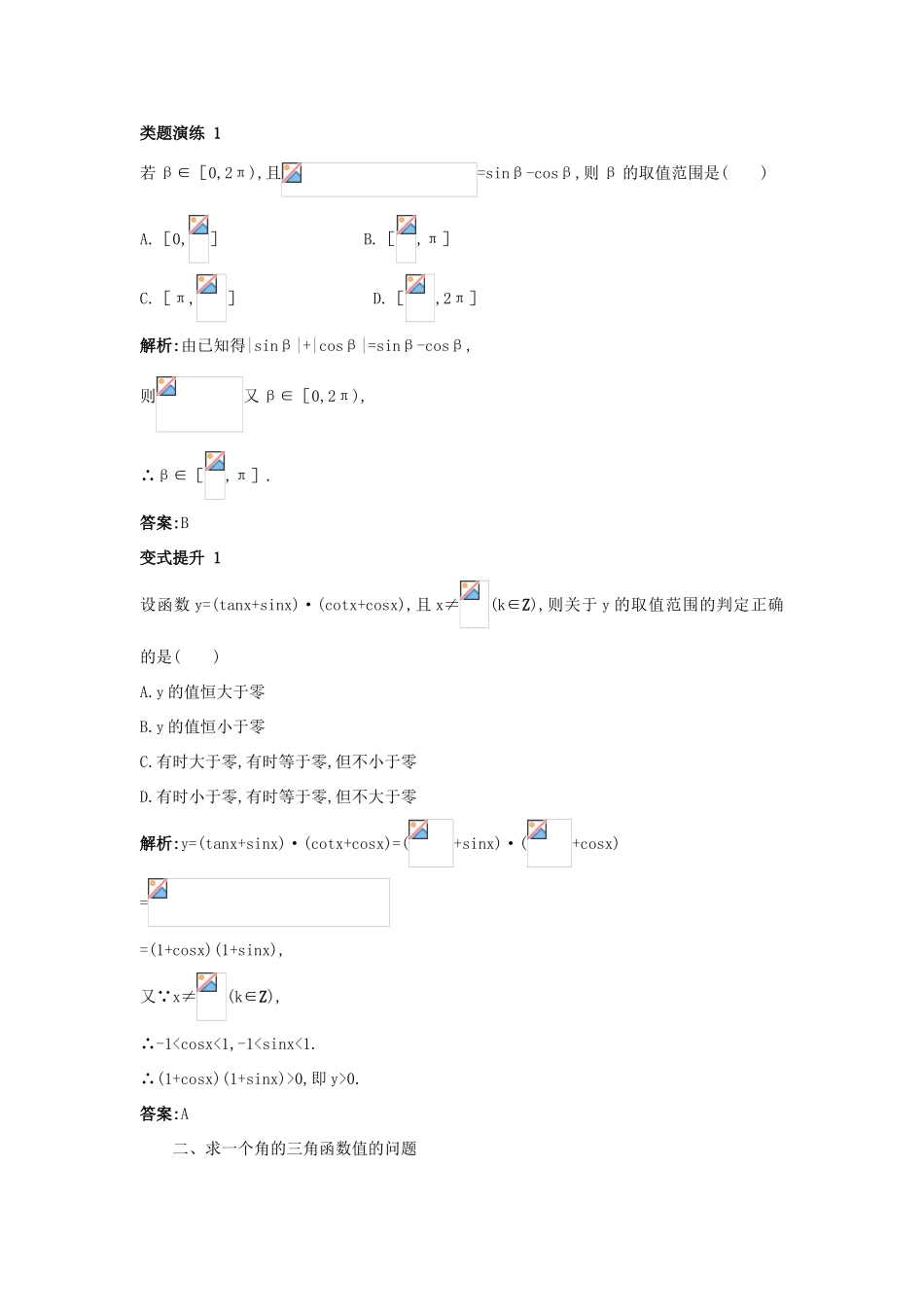
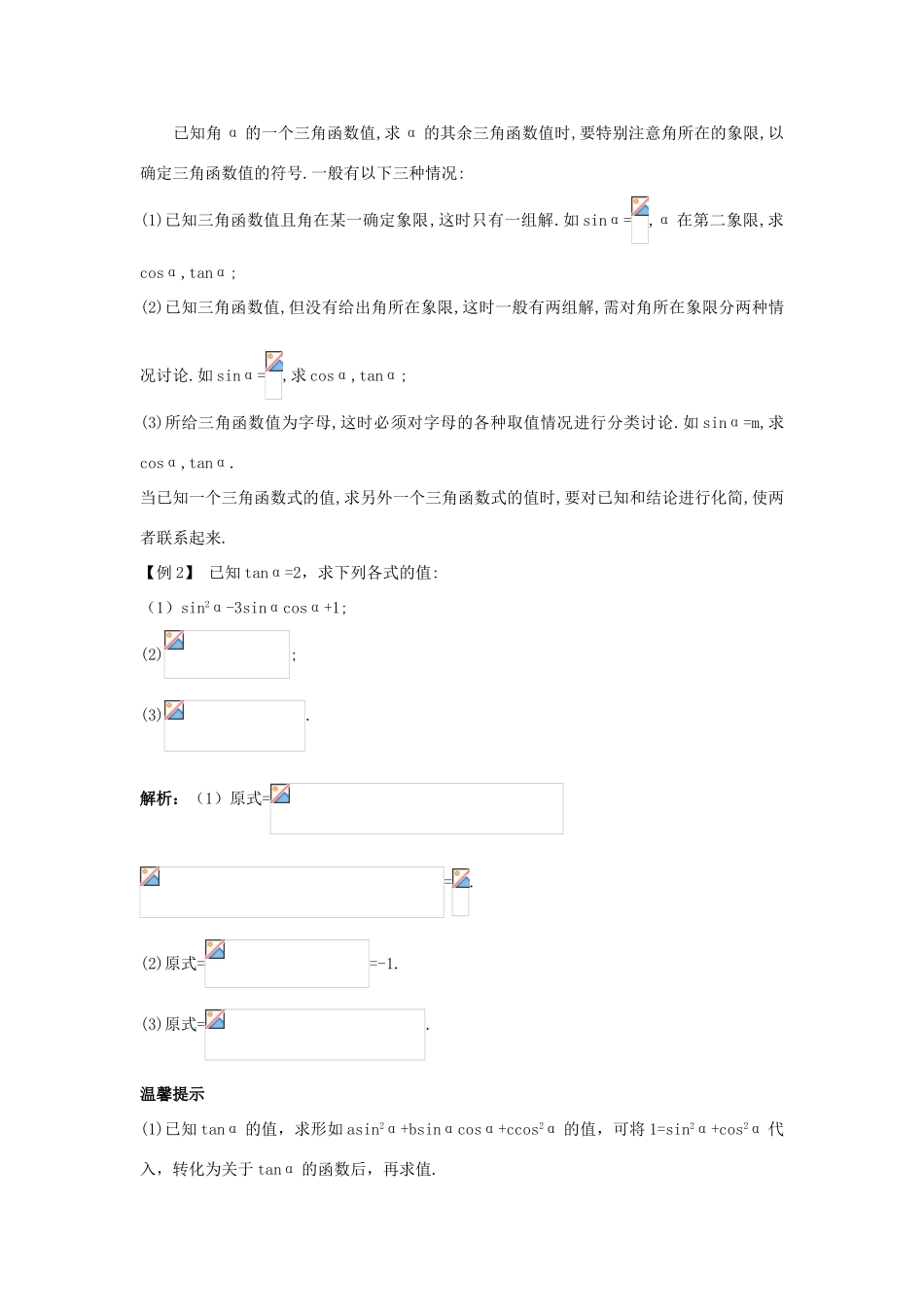
1.2.3 同角三角函数的基本关系式课堂导学三点剖析 一、对基本关系的理解(1)公式 sin2α+cos2α=1(平方关系)和=tanα(商数关系),称为同角三角函数的基本关系式.这里,“同角”有两层含义,一是“角相同”,二是对“任意”一个角(在使得函数有意义的前提下)关系式都成立.(2)sin2α 是(sinα)2的简写,读作“sinα 的平方”,不能将 sin2α 写成 sinα2,前者是 α的正弦的平方,后者是 α 的平方的正弦,两者是不同的.应弄清它们的区别,并能正确书写.(3) 公 式 sin2α+cos2α=1,=tanα 的 应 用 极 为 广 泛 , 它 们 还 有 如 下 等 价 形式:sin2α=1-cos2α,cos2α=1-sin2α,sinα=cosαtanα,cosα=.【例 1】 若 sinθ+cosθ=-1(θ≠,k∈Z),则 θ 所在象限是( )A.第一象限 B.第二象限C.第三象限 D.第四象限解析:记 f(θ)=sinθ+cosθ.(1)当 θ 在第一象限时,sinθ>0,cosθ>0.∴f(θ)=1;(2)当 θ 在第二象限时,sinθ>0,cosθ<0.∴f(θ)=sin2θ-cos2θ;(3)当 θ 在第三象限时,sinθ<0,cosθ<0.∴f(θ)=-1;(4)当 θ 在第四象限时,sinθ<0,cosθ>0.∴f(θ)=-sin2θ+cos2θ.答案:C各个击破类题演练 1若 β∈[0,2π),且=sinβ-cosβ,则 β 的取值范围是( )A.[0,] B.[,π]C.[π,] D.[,2π]解析:由已知得|sinβ|+|cosβ|=sinβ-cosβ,则又 β∈[0,2π),∴β∈[,π].答案:B变式提升 1设函数 y=(tanx+sinx)·(cotx+cosx),且 x≠(k∈Z),则关于 y 的取值范围的判定正确的是( )A.y 的值恒大于零B.y 的值恒小于零C.有时大于零,有时等于零,但不小于零D.有时小于零,有时等于零,但不大于零解析:y=(tanx+sinx)·(cotx+cosx)=(+sinx)·(+cosx)==(1+cosx)(1+sinx),又 x≠(k∈Z),∴-10,即 y>0.答案:A 二、求一个角的三角函数值的问题 已知角 α 的一个三角函数值,求 α 的其余三角函数值时,要特别注意角所在的象限,以确定三角函数值的符号.一般有以下三种情况:(1)已知三角函数值且角在某一确定象限,这时只有一组解.如 sinα=,α 在第二象限,求cosα,tanα;(2)已知三角函数值,但没有给出角所在象限,这时一般有两组解,需对角所在象限分两种情况讨论.如 sinα=,求 cosα,tanα;(3)所给三角函数值为字母,这时必须对字母的各种取值情况进行分类讨论.如 sinα=m,求cosα,tanα.当已知一个三角函数式的值,求另外一个三角函数式的值时,要对已知和结论...