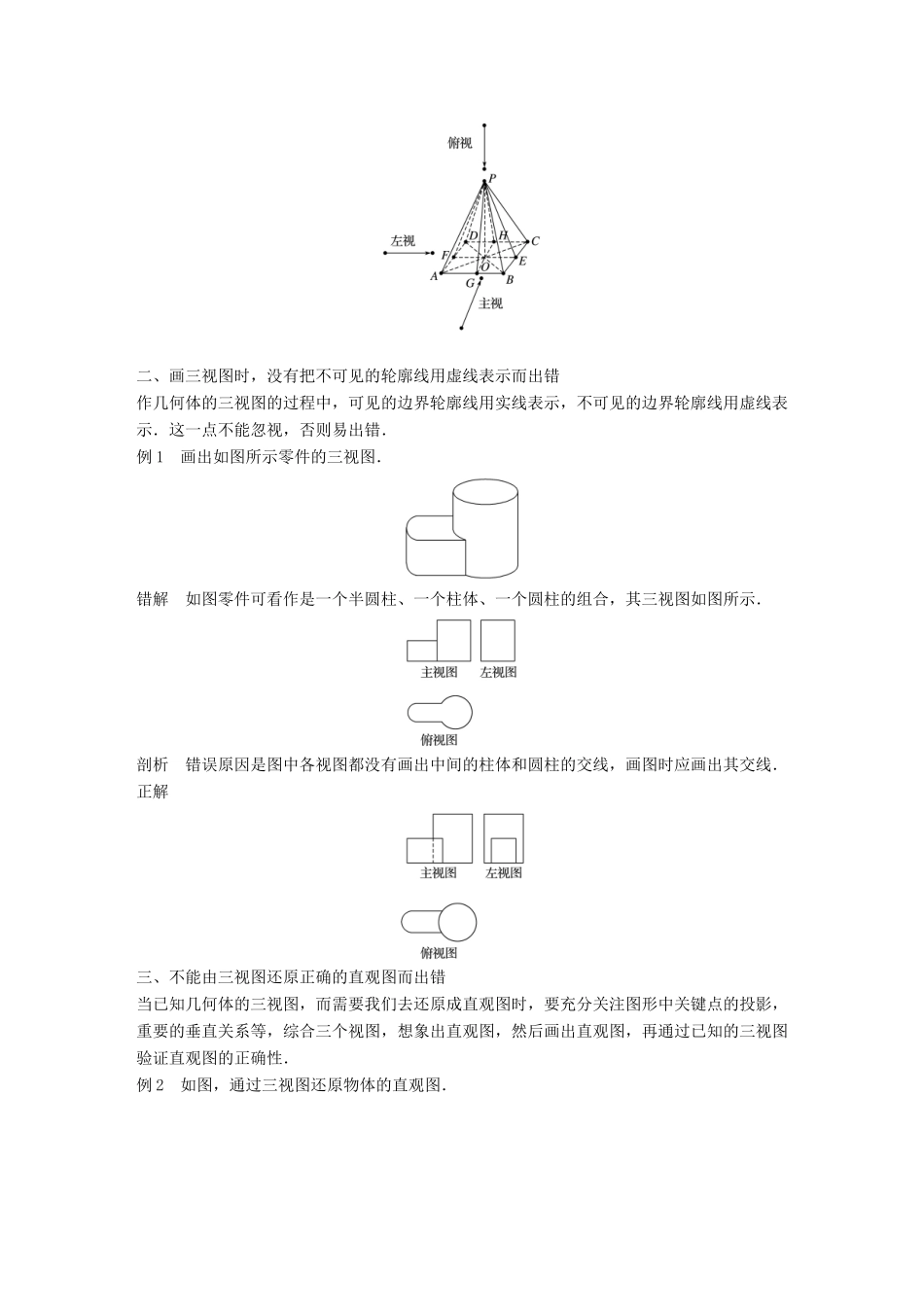
第一章 立体几何初步1 学习空间几何体要“三会”一、会辨别例 1 下列说法:①一个几何体有五个面,则该几何体可能是球、棱锥、棱台、棱柱;②若一个几何体有两个面平行,且其余各面均为梯形,则它一定是棱台;③直角三角形绕其任意一条边旋转一周都可以围成圆锥.其中说法正确的个数为________.分析 可根据柱体、锥体、台体和球体的概念进行判断.解析 一个几何体有五个面,可能是四棱锥、三棱台,也可能是三棱柱,但不可能是球,所以①错;由于棱台的侧棱是原棱锥侧棱的一部分,所以棱台的各侧棱的延长线相交于一点,而②中的几何体其侧棱延长线并不一定会交于一点,所以②错;③中如绕直角边旋转可以形成圆锥,但绕斜边旋转形成的是由两个圆锥组成的组合体,所以③错.故填 0.答案 0评注 要准确辨别各种几何体,可从轴、侧面、底面、母线、平行于底面的截面等方面入手,当然掌握定义是大前提.二、会折展例 2 纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北.现在沿该正方体的一些棱将正方体剪开,外面朝上展平,得到如图所示的平面图形,则标“Δ”的面的方位是________.分析 将平面展开图按要求折叠成正方体,根据方位判断即可.解析 将平面展开图折叠成正方体,如图所示,标“Δ”的面的方位应为北.故填北.答案 北评注 将空间几何体展开成平面图形,或将展开图折叠成空间几何体,在后面的计算或证明中经常用到,应引起重视.解决这类问题的关键是充分发挥空间想象能力或亲自动手制作模型进行实践.三、会割补例 3 如图所示是一个三棱台 ABC-A1B1C1.试用一个平面把这个三棱台分成一个三棱柱和一个多面体,并用字母表示.分析 三棱柱要求两个底面为平行且全等的三角形,其余三个面为四边形,且相邻两个四边形的公共边都相互平行.解 作 A1D∥BB1,C1E∥BB1,连接 DE,则三棱柱为 A1B1C1-DBE,多面体为 ADECC1A1(如图所示).评注 正确理解各类几何体的概念是将几何体进行割补的前提,在后面的空间几何体的体积或面积计算中经常要通过线、面,将不规则的几何体通过割补的方法转化为规则的几何体,从而可以利用公式求解.2 三视图易错点剖析一、棱锥的视图易出错我们在画正三棱锥、正四棱锥时要注意从不同角度得到的三视图.实际上,在上述几何体的三视图中,左视图最容易出错,在画这些常见锥体的三视图时,可做出几何体的高线,有了高线的衬托,自然就可以得到正确的三视图.如图,对于正三棱...