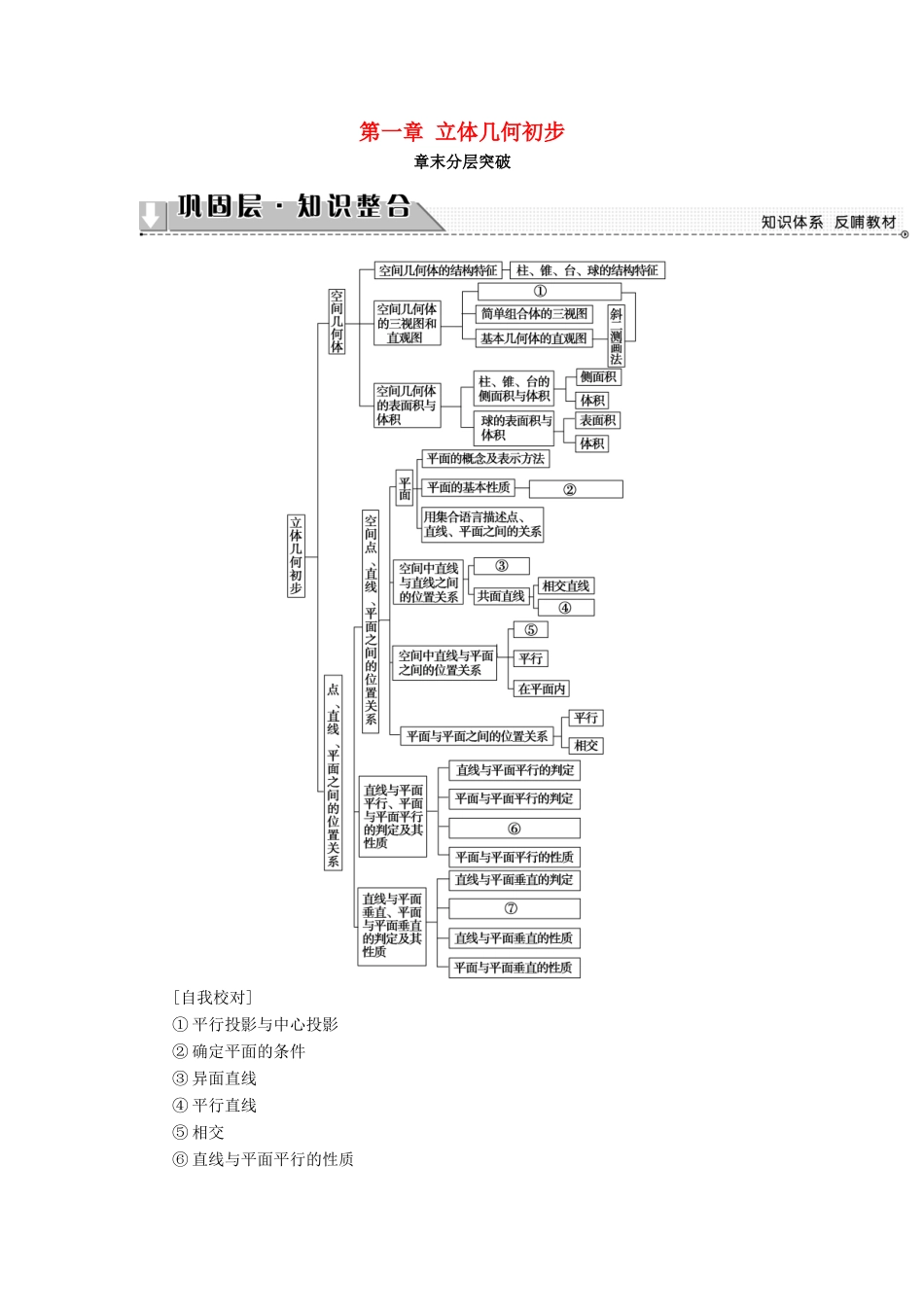
第一章 立体几何初步章末分层突破[自我校对]① 平行投影与中心投影② 确定平面的条件③ 异面直线④ 平行直线⑤ 相交⑥ 直线与平面平行的性质⑦ 平面与平面垂直的判定 (教师用书独具)空间几何体的三视图与直观图三视图和直观图是空间几何体的不同表现形式,空间几何体的三视图可以使我们很好地把握空间几何体的性质.由空间几何体可以画出它的三视图,同样,由三视图可以想象出空间几何体的形状,两者之间可以相互转化. 若某几何体的三视图如图 11 所示,则这个几何体的直观图可以是( ) 【导学号:45722062】图 11A B C D 【精彩点拨】 ――→――→【规范解答】 所给选项中,A、C 选项的主视图、俯视图不符合,D 选项的左视图不符合,只有 B 选项符合.【答案】 B[再练一题]1.一个由半球和四棱锥组成的几何体,其三视图如图 12 所示,则该几何体的体积为( )图 12A.+π B.+π C.+π D.1+π【解析】 由三视图及四棱锥与球的体积公式求解.由三视图知,该四棱锥是底面边长为 1,高为 1 的正四棱锥,结合三视图可得半球半径为,从而该几何体的体积为×12×1+×π×=+π.故选 C.【答案】 C空间几何体的表面积、体积1.几何体的表面积及体积的计算是现实生活中经常能够遇到的问题,在计算中应注意各数量之间的关系及各元素之间的位置关系,特别是特殊的柱、锥、台,要注意其中矩形、梯形及直角三角形等重要的平面图形的作用.2.常见的计算方法(1)公式法:根据题意直接套用表面积或体积公式求解.(2)割补法:割补法的思想是通过分割或补形,将原几何体分割成或补成较易计算体积的几何体,从而求出原几何体的体积.(3)等体积变换法:等积变换法的思想是从不同的角度看待原几何体,通过改变顶点和底面,利用体积不变的原理,来求原几何体的体积. 如图 13,四棱锥 PABCD 的底面 ABCD 是边长为 2 的菱形,∠BAD=60°,已知PB=PD=2,PA=.图 13(1)证明:PC⊥BD;(2)若 E 为 PA 的中点,求三棱锥 PBCE 的体积.【精彩点拨】 (1)连接 AC,与 BD 交于点 O,由 PB=PD 以及底面为菱形的条件,由线面垂直的判定定理可证 BD⊥平面 APC,从而可证;(2)利用四面体的等积变换,转化为以 B为顶点的三棱锥,进而判断三棱锥 P—BCE 的体积是三棱锥 B—APC 的体积的一半,代入公式计算.【规范解答】 (1)证明 连接 AC,交 BD 于点 O,连接 PO.因为底面 ABCD 是菱形,所以 AC⊥BD,BO=DO.由...