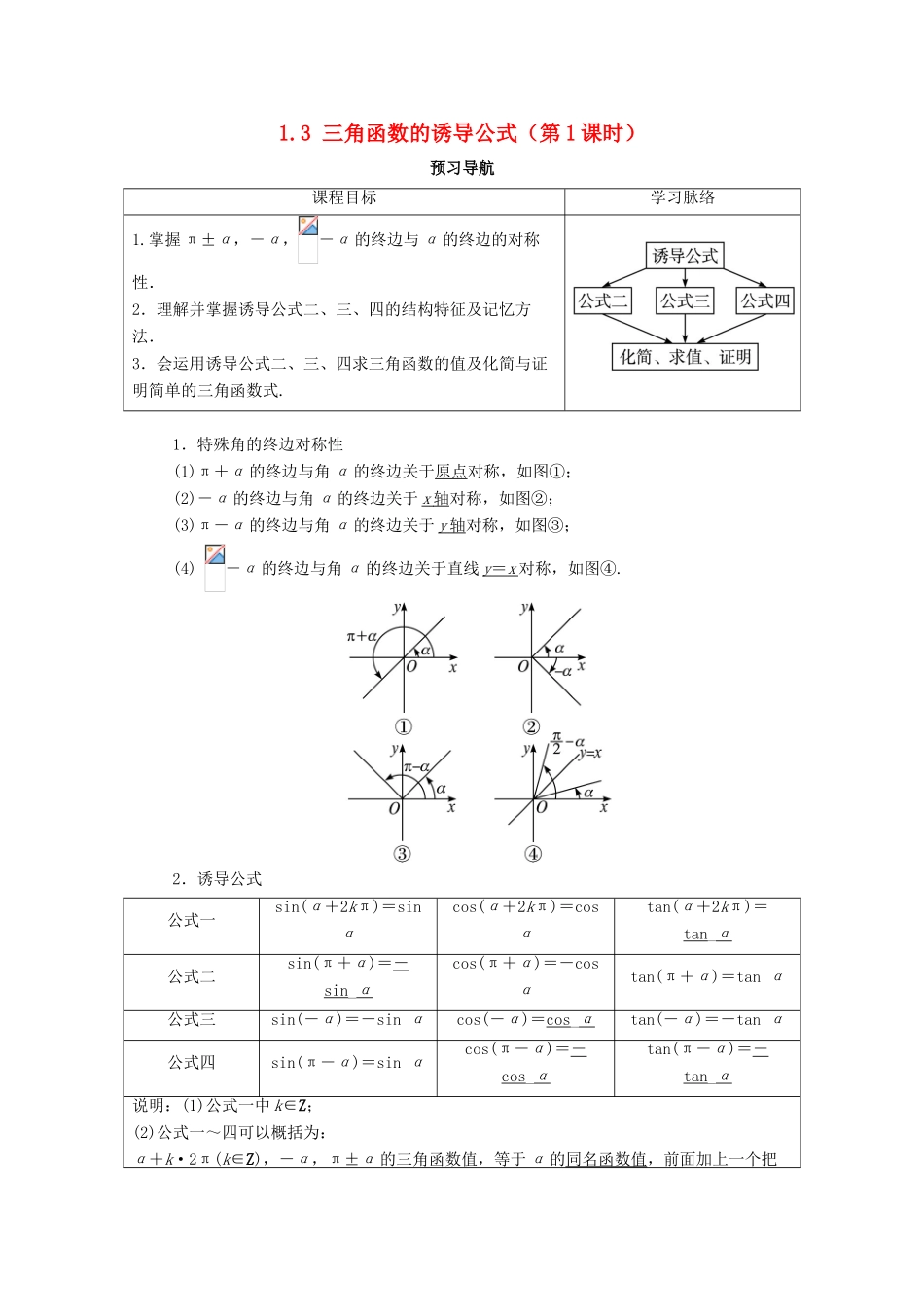
1.3 三角函数的诱导公式(第 1 课时)预习导航课程目标学习脉络1.掌握 π±α,-α,-α 的终边与 α 的终边的对称性.2.理解并掌握诱导公式二、三、四的结构特征及记忆方法.3.会运用诱导公式二、三、四求三角函数的值及化简与证明简单的三角函数式. 1.特殊角的终边对称性(1)π+α 的终边与角 α 的终边关于原点对称,如图①;(2)-α 的终边与角 α 的终边关于 x 轴 对称,如图②;(3)π-α 的终边与角 α 的终边关于 y 轴 对称,如图③;(4) -α 的终边与角 α 的终边关于直线 y = x 对称,如图④.2.诱导公式公式一sin(α+2kπ)=sin αcos(α+2kπ)=cos αtan(α+2kπ)=tan_α公式二sin(π+α)=-sin_αcos(π+α)=-cos αtan(π+α)=tan α公式三sin(-α)=-sin αcos(-α)=cos_αtan(-α)=-tan α公式四sin(π-α)=sin αcos(π-α)=-cos_αtan(π-α)=-tan_α说明:(1)公式一中 k∈Z;(2)公式一~四可以概括为:α+k·2π(k∈Z),-α,π±α 的三角函数值,等于 α 的同名函数值,前面加上一个把α 看成锐角时原函数值的符号思考 1 若 α 是第三象限角,则 sin(π-α)=sin α 成立吗?提示:公式 sin(π-α)=sin α 中的 α 是任意角,不因角 α 所在的象限而改变三角函数值,所以无论 α 是第几象限角,都有 sin(π-α)=sin α.思考 2 存在 α∈R,使 sin(π+α)=sin α 成立吗?提示:存在 α=kπ,k∈Z,使 sin(π+α)=sin α=0 成立.思考 3 诱导公式二、三、四的记忆口诀是什么?提示:函数名不变,符号看象限.3.公式一~四的应用思考 4 上述步骤的记忆口诀是什么?提示:负化正,大化小,化到锐角再求值,体现了化归思想.