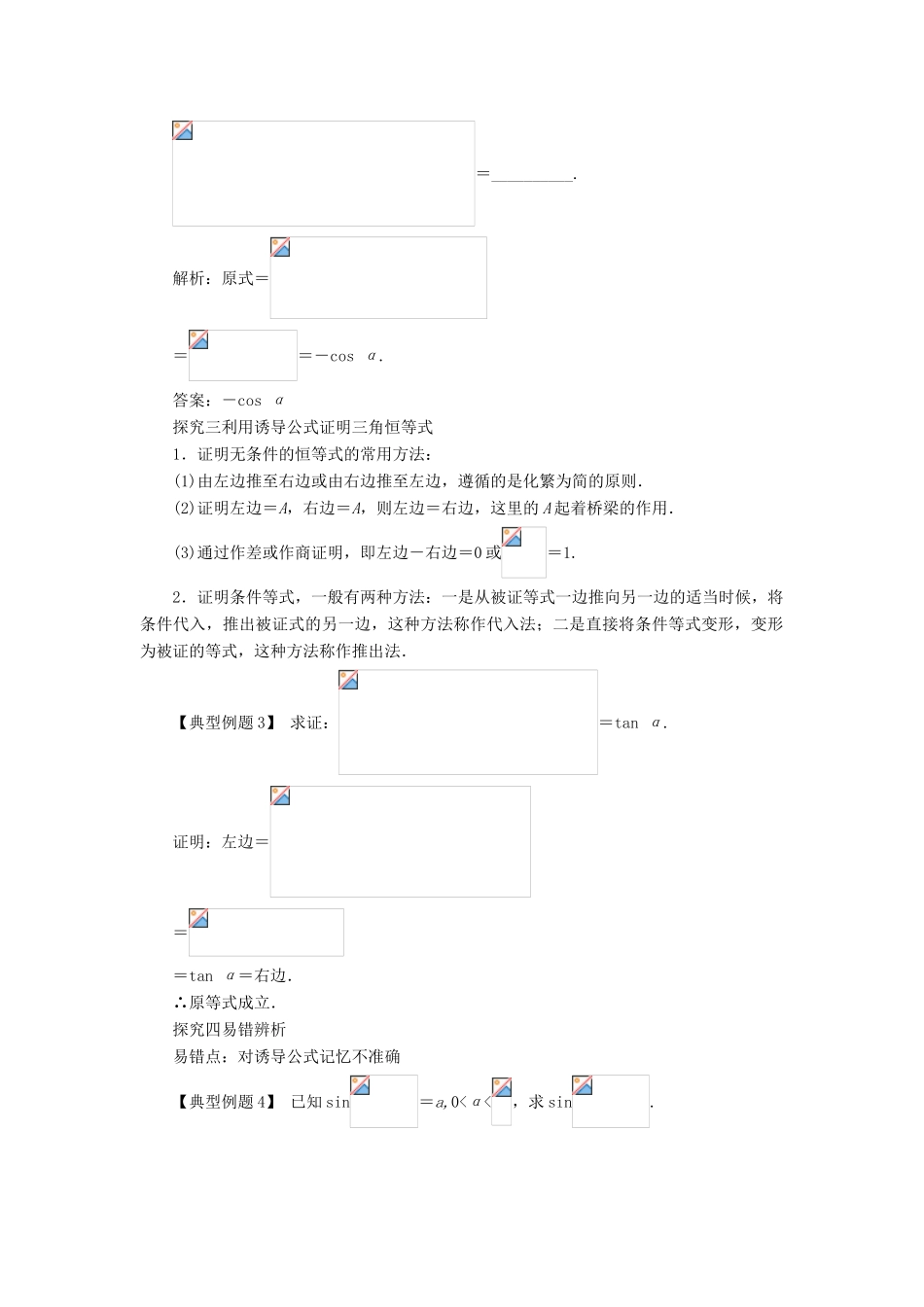
1.3 三角函数的诱导公式(第 2 课时)课堂探究探究一 利用诱导公式求值已知一三角函数值求其他三角函数值的解题思路:(1)观察:①观察已知的角和所求角的差异,寻求角之间的关系;② 观察已知的三角函数名与所求的三角函数名的差异.(2)转化:运用诱导公式将不同的角转化为相同的角;将不同名的三角函数化为同名的三角函数.【典型例题 1】 (1)已知 sin=,则 sin=( )A. B.- C. D.-(2)计算:sin21°+sin22°+sin288°+sin289°=__________.解析:(1)∵sin=,∴cos α=.又∵sin=-cos α,∴sin=-.故选 B.(2)∵1°+89°=90°,2°+88°=90°,∴sin 89°=sin(90°-1°)=cos 1°,sin 88°=sin(90°-2°)=cos 2°.∴sin21°+sin22°+sin288°+sin289°=sin21°+sin22°+cos21°+cos22°=2.答案:(1)B (2)2探究二 化简三角函数式三角函数式化简的方法和技巧:(1)方法:三角函数式化简的关键是抓住函数名称之间的关系和角之间的关系,据此灵活应用相关的公式及变形,解决问题.(2)技巧:①异名化同名;②异角化同角;③切化弦.【典型例题 2】 化简:=__________.解析:原式===-cos α.答案:-cos α探究三利用诱导公式证明三角恒等式1.证明无条件的恒等式的常用方法:(1)由左边推至右边或由右边推至左边,遵循的是化繁为简的原则.(2)证明左边=A,右边=A,则左边=右边,这里的 A 起着桥梁的作用.(3)通过作差或作商证明,即左边-右边=0 或=1.2.证明条件等式,一般有两种方法:一是从被证等式一边推向另一边的适当时候,将条件代入,推出被证式的另一边,这种方法称作代入法;二是直接将条件等式变形,变形为被证的等式,这种方法称作推出法.【典型例题 3】 求证:=tan α.证明:左边===tan α=右边.∴原等式成立.探究四易错辨析易错点:对诱导公式记忆不准确【典型例题 4】 已知 sin=a,0<α<,求 sin.错解:∵0<α<,∴-<-α<,∴cos>0,∴cos==,sin=sin=cos=.错因分析:对使用诱导公式求三角函数值时,符号的确定掌握不好,在 sin 中,要把“-α”看成锐角来确定三角函数值的符号.正解:∵0<α<,∴-<-α<,∴cos>0.∴cos==.∴sin=sin=-cos=-.