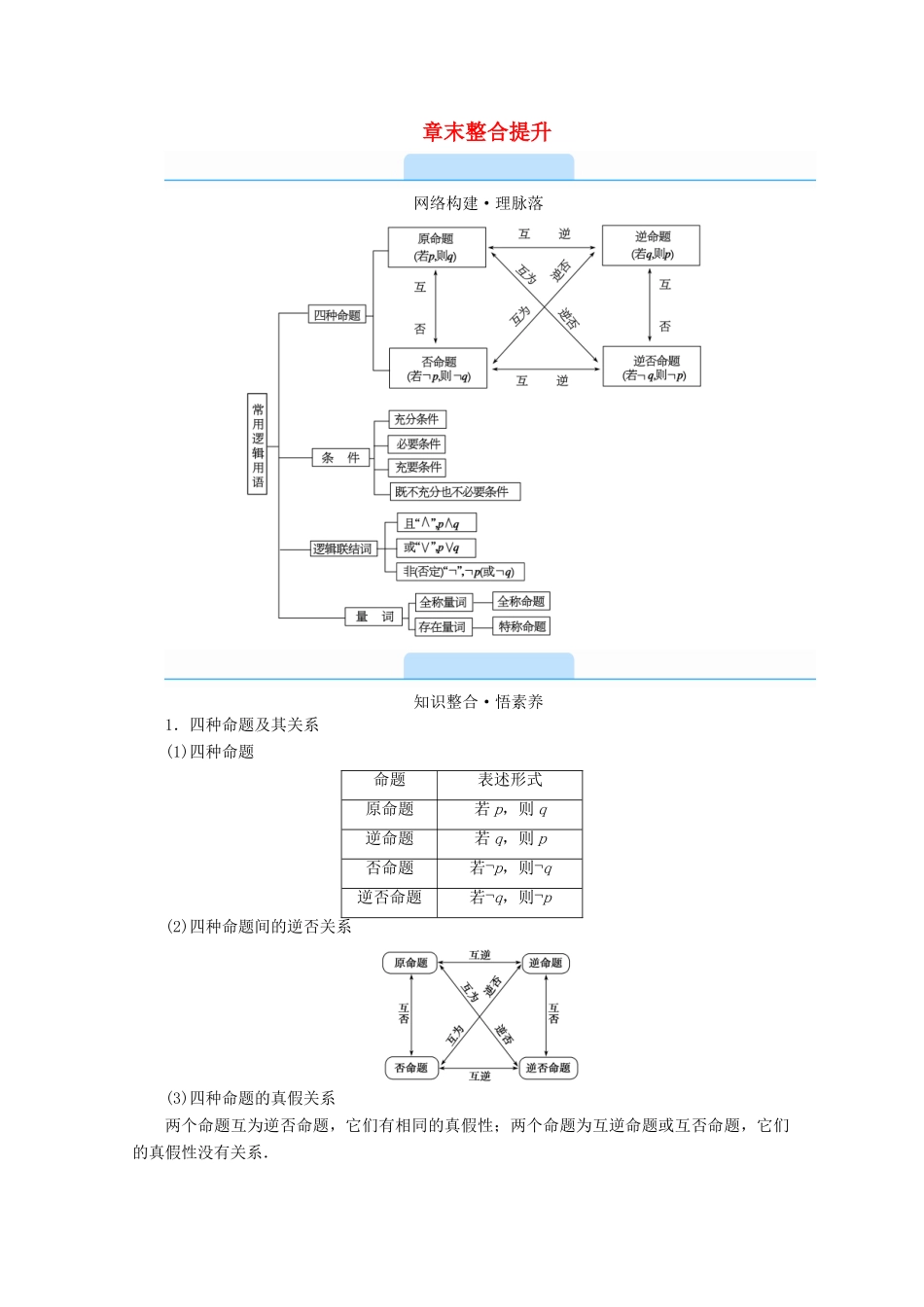
章末整合提升网络构建·理脉落知识整合·悟素养1.四种命题及其关系(1)四种命题命题表述形式原命题若 p,则 q逆命题若 q,则 p否命题若¬p,则¬q逆否命题若¬q,则¬p(2)四种命题间的逆否关系(3)四种命题的真假关系两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.2.充分条件与必要条件(1)如果 p⇒q,那么称 p 是 q 的充分条件,q 是 p 的必要条件.(2)分类:①p 是 q 的充要条件:p⇒q 且 q⇒p,记作 p⇔q;②p 是 q 的充分不必要条件:p⇒q,q⇒p;③p 是 q 的必要不充分条件:q⇒p,p⇒q;④p 是 q 的既不充分也不必要条件:p⇒q 且 q⇒p.3.简单的逻辑联结词(1)用联结词“且”“或”“非”联结命题 p 和命题 q,可得 p∧q,p∨q,¬p.(2)命题 p∧q 中 p、q 有一假为假,p∨q 有一真为真,p 与¬p 必定是一真一假.4.全称量词与存在量词(1)全称量词与全称命题.全称量词用符号“∀”表示.全称命题用符号简记为∀x∈M,p(x).(2)存在量词与特称命题.存在量词用符号“∃”表示.特称命题用符号简记为∃x0∈M,p(x0).5.含有一个量词的命题的否定命题命题的否定∀x∈M,p(x)∃x0∈M,¬p(x0)∃x0∈M,p(x0)∀x∈M,¬p(x)专题突破·启智能专题 命题及其真假判断可以判断真假的陈述句为命题、反问句也是命题,但疑问句、祈使句、感叹句都不是命题.典例 1 下列语句哪些是命题,是命题的判断其真假.(1)方程 x2-2x=0 的根是自然数;(2)sin(α+β)=sinα+sinβ(α,β 是任意角);(3)垂直于同一个平面的两个平面平行;(4)函数 y=12x+1 是单调增函数;(5)非典型肺炎是怎样传染的?(6)奇数的平方仍是奇数;(7)好人一生平安!(8)解方程 3x+1=0;(9)方程 3x+1=0 只有一个解;(10)3x+1=0.[解析] (1)(2)(3)(4)(6)(9)都是命题,其中(1)(4)(6)(9)为真命题.『规律总结』 (5)是疑问句,(7)是感叹句,(8)是祈使句都不是命题,(10)中由于 x 的值未给,故无法判断此句的真假,因而不是命题.典例 2 判断命题:“若 a+b≠7,则 a≠3,且 b≠4”的真假.[解析] 其逆否命题为:“若 a=3 或 b=4,则 a+b=7”.显然这是一个假命题,∴原命题为假.『规律总结』 复合命题的真假判断是个难点,当直接判断不易着手时,可转为判断它的等价命题——逆否命题,这是一种重要的处理技巧.专题 四种命题的关系1.注意:若 p...