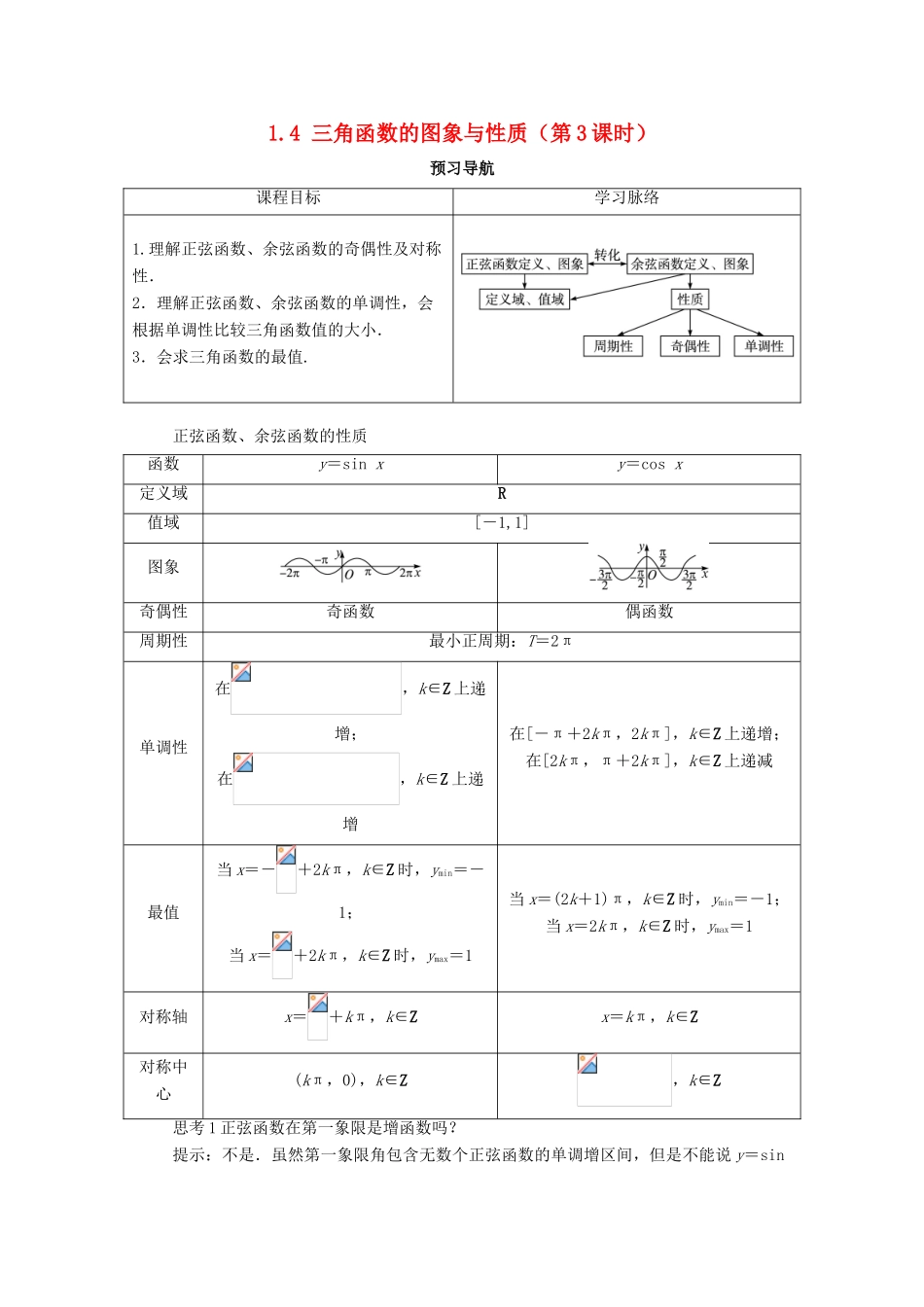
1.4 三角函数的图象与性质(第 3 课时)预习导航课程目标学习脉络1.理解正弦函数、余弦函数的奇偶性及对称性.2.理解正弦函数、余弦函数的单调性,会根据单调性比较三角函数值的大小.3.会求三角函数的最值. 正弦函数、余弦函数的性质函数y=sin xy=cos x定义域R值域[-1,1]图象奇偶性奇函数偶函数周期性最小正周期:T=2π单调性在,k∈Z 上递增;在,k∈Z 上递增在[-π+2kπ,2kπ],k∈Z 上递增;在[2kπ,π+2kπ],k∈Z 上递减最值当 x=-+2kπ,k∈Z 时,ymin=-1;当 x=+2kπ,k∈Z 时,ymax=1当 x=(2k+1)π,k∈Z 时,ymin=-1;当 x=2kπ,k∈Z 时,ymax=1对称轴x=+kπ,k∈Zx=kπ,k∈Z对称中心(kπ,0),k∈Z,k∈Z思考 1 正弦函数在第一象限是增函数吗?提示:不是.虽然第一象限角包含无数个正弦函数的单调增区间,但是不能说 y=sin x 在第一象限是增函数,比如,都是第一象限角且<,却有 sin=sin.思考 2 正弦曲线、余弦曲线的对称轴、对称中心分别有什么特点?提示:正弦曲线、余弦曲线的对称轴分别过曲线的最高点或最低点,正弦曲线的对称轴为 x=kπ+ (k∈Z),余弦曲线的对称轴为 x=kπ(k∈Z);而它们的对称中心分别过正弦曲线、余弦曲线与 x 轴的交点,因此,正弦曲线的对称中心是(kπ,0)(k∈Z),余弦曲线的对称中心是 (k∈Z).