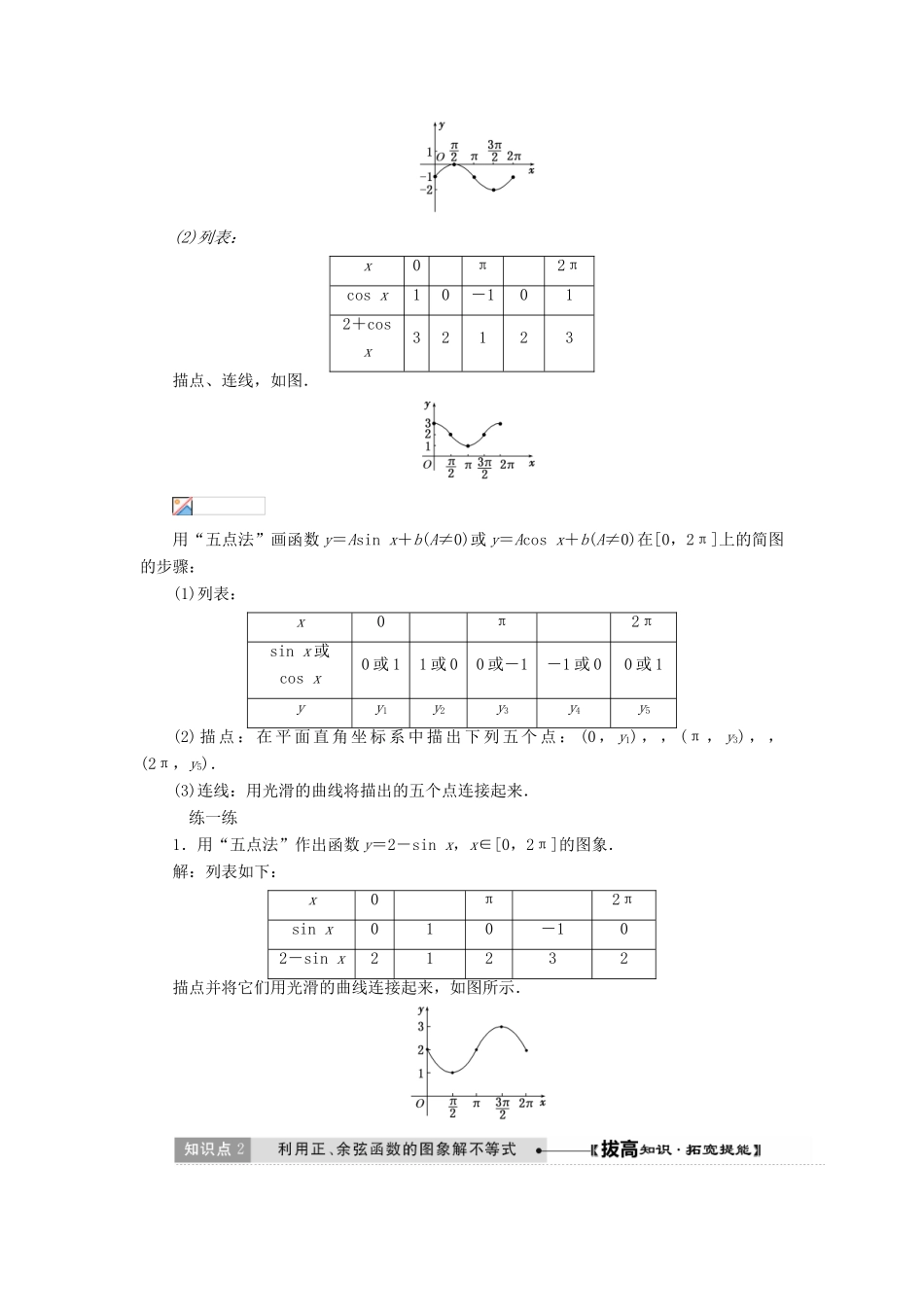
1.4 三角函数的图象与性质第 1 课时 正弦函数、余弦函数的图象[核心必知]1.预习教材,问题导入根据以下提纲,预习教材 P30~P33的内容,回答下列问题.(1)观察教材 P31图 1.4-3,你认为正弦曲线是如何画出来的?提示:利用单位圆中的正弦线可以作出 y = sin _x , x ∈ [0 , 2π ] 的图象 , 将 y = sin _x在 [0 , 2π ] 内的图象左右平移即可得到正弦曲线 .(2)在作正弦函数的图象时,应抓住哪些关键点?提示:作正弦函数 y = sin _x , x ∈ [0 , 2π ] 的图象时 , 起关键作用的点有以下五个: (0 , 0 ) ,, ( π , 0 ) ,, (2 π , 0 ) .(3)作余弦函数的图象时,应抓住哪些关键点?提示:作余弦函数 y = cos _x , x ∈ [0 , 2π ] 的图象时 , 起关键作用的点有以下五个: (0 , 1 ) ,, ( π , - 1) ,, (2 π , 1 ) .2.归纳总结,核心必记(1)正弦曲线正弦函数 y=sin x,x∈R 的图象叫正弦曲线.(2)正弦函数图象的画法① 几何法:(ⅰ)利用正弦线画出 y=sin x,x∈[0,2π]的图象;(ⅱ)将图象向左、向右平行移动(每次 2π 个单位长度).② 五点法:(ⅰ)画出正弦曲线在 [0,2π]上的图象的五个关键点 (0 , 0 ) ,,( π , 0 ) ,,(2 π , 0 ) ,用光滑的曲线连接;(ⅱ)将所得图象向左、向右平行移动(每次 2π 个单位长度).(3)余弦曲线余弦函数 y=cos x,x∈R 的图象叫余弦曲线.(4)余弦函数图象的画法① 要得到 y=cos x 的图象,只需把 y=sin x 的图象向左平移个单位长度即可,这是由于 cos x=sin.② 用“五点法”:画余弦曲线 y=cos x 在[0,2π]上的图象时,所取的五个关键点分别为(0 , 1 ) ,,( π , - 1) ,,(2 π , 1 ) ,再用光滑的曲线连接.[问题思考](1)正弦曲线和余弦曲线是向左右两边无限延伸的吗?提示:是.(2)余弦曲线与正弦曲线完全一样吗?提示:余弦曲线与正弦曲线形状相同 , 但在同一坐标系下的位置不同 .[课前反思](1)正弦曲线的定义: ;(2)正弦曲线的画法: ;(3)余弦曲线的定义: ;(4)余弦曲线的画法: .讲一讲1.用“五点法”作出下列函数的简图:(1)y=sin x-1,x∈[0,2π];(2)y=2+cos x,x∈[0,2π].[尝试解答] (1)列表:x0π2πsin x010-10sin x-1-10-1-2-1描点、连线,如图....