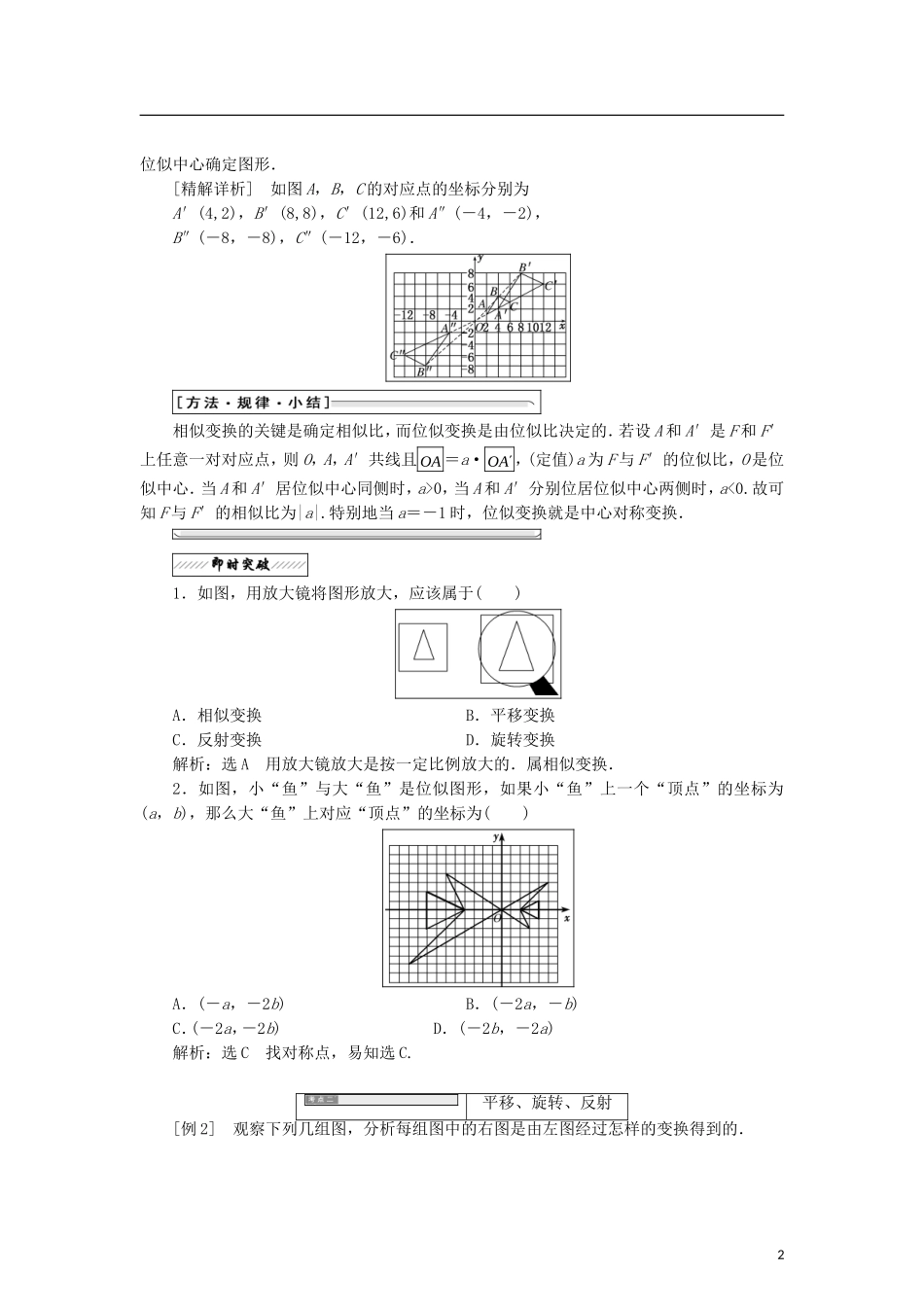
第一课时 平移、旋转、反射和相似与位似[对应学生用书 P1]1.平移、旋转、反射变换含义平移图形的平移过程称为平移变换旋转图形的旋转过程称为旋转变换反射一个图形 F 绕一条直线 l 翻转 180°得到另外一个图形 F′,则 F 与 F′关于 l对称,这种图形的变化过程称为反射变换,直线 l 称为反射轴2.相似与位似变换含义相似两个图形的形状相同,但大小不同,这两个图形是相似图形,把一个图形按一定比例放大或缩小,这种图形的变化过程称为相似变换位似把一个图形变为它的位似图形,这种图形的变化过程称为位似变换1.平移、旋转变换过程中有何异同点?提示:相同点:两者不改变图形的形状和大小.不同点:平移不会改变图形的方向,而旋转改变图形方向.2.反射变换其实质是轴对称变换对吗?提示:对.反射变换其实质就是轴对称变换.反射是由一条反射线确定,反射线也叫对称轴,是连接图形中任一点与该点映象之间的所有线段的垂直平分线.3.位似变换是特殊的相似变换吗?提示:相似变换是把一个图形按一定比例放大或缩小,而位似变换是图形的位置发生了改变,其形状、对应角的大小都不变.位似变换是一种特殊的相似变换.[对应学生用书 P1]相似与位似变换及应用[例 1] 如图,△ABC 三个顶点坐标分别为 A(2,1),B(4,4),C(6,3),以点 O 为位似中心,相似比为 2,将△ABC 放大,位似变换后,求 A,B,C 的对应点的坐标.[思路点拨] 本题主要考查相似和位似变换,解答此题需要先利用相似变换后再利用1位似中心确定图形.[精解详析] 如图 A,B,C 的对应点的坐标分别为A′(4,2),B′(8,8),C′(12,6)和 A″(-4,-2),B″(-8,-8),C″(-12,-6).相似变换的关键是确定相似比,而位似变换是由位似比决定的.若设 A 和 A′是 F 和 F′上任意一对对应点,则 O,A,A′共线且 OA�=a· OA�,(定值)a 为 F 与 F′的位似比,O 是位似中心.当 A 和 A′居位似中心同侧时,a>0,当 A 和 A′分别位居位似中心两侧时,a<0.故可知 F 与 F′的相似比为|a|.特别地当 a=-1 时,位似变换就是中心对称变换.1.如图,用放大镜将图形放大,应该属于( )A.相似变换 B.平移变换C.反射变换 D.旋转变换解析:选 A 用放大镜放大是按一定比例放大的.属相似变换.2.如图,小“鱼”与大“鱼”是位似图形,如果小“鱼”上一个“顶点”的坐标为(a,b),那么大“鱼”上对应“顶点”的坐标为( )A.(...