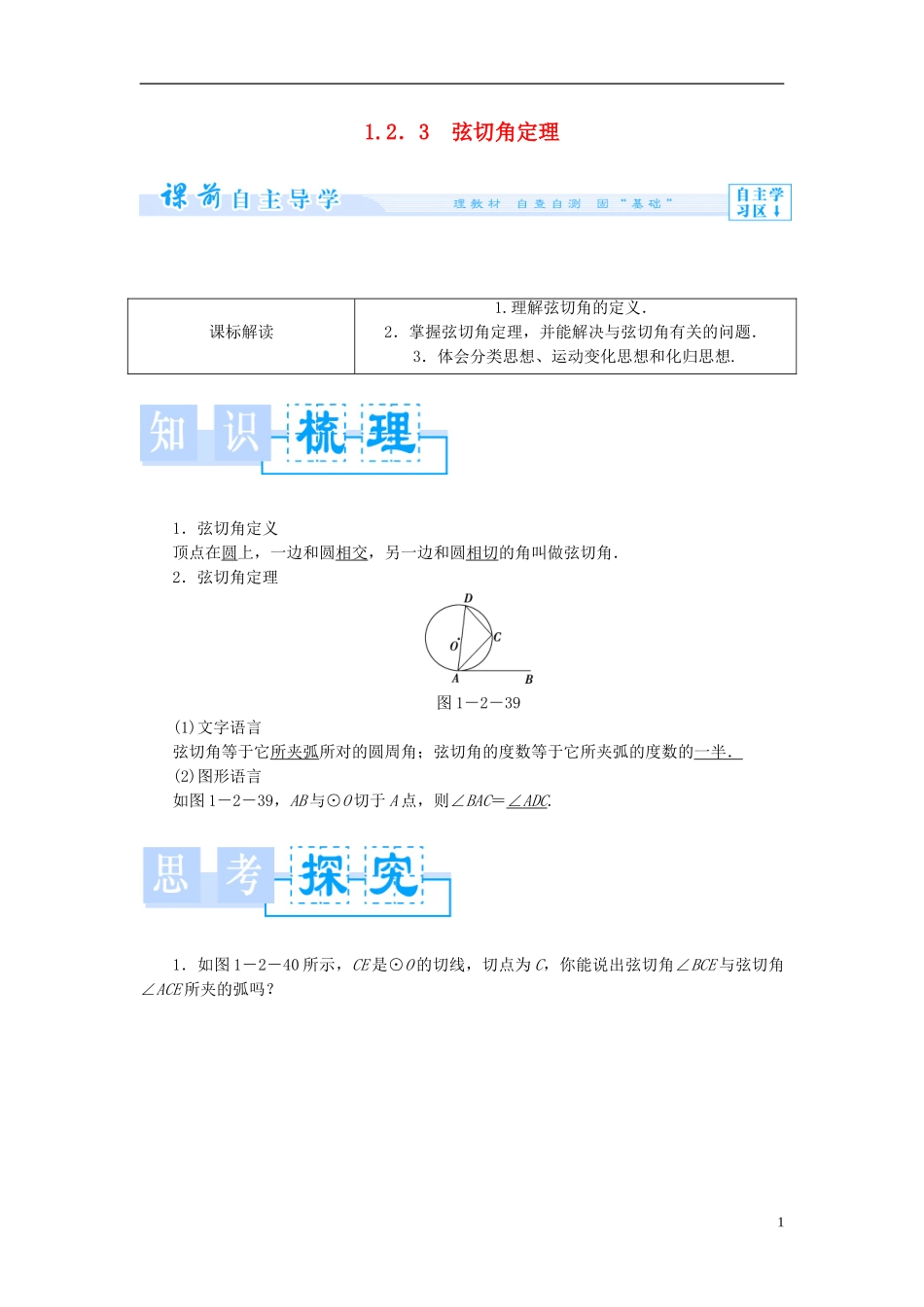
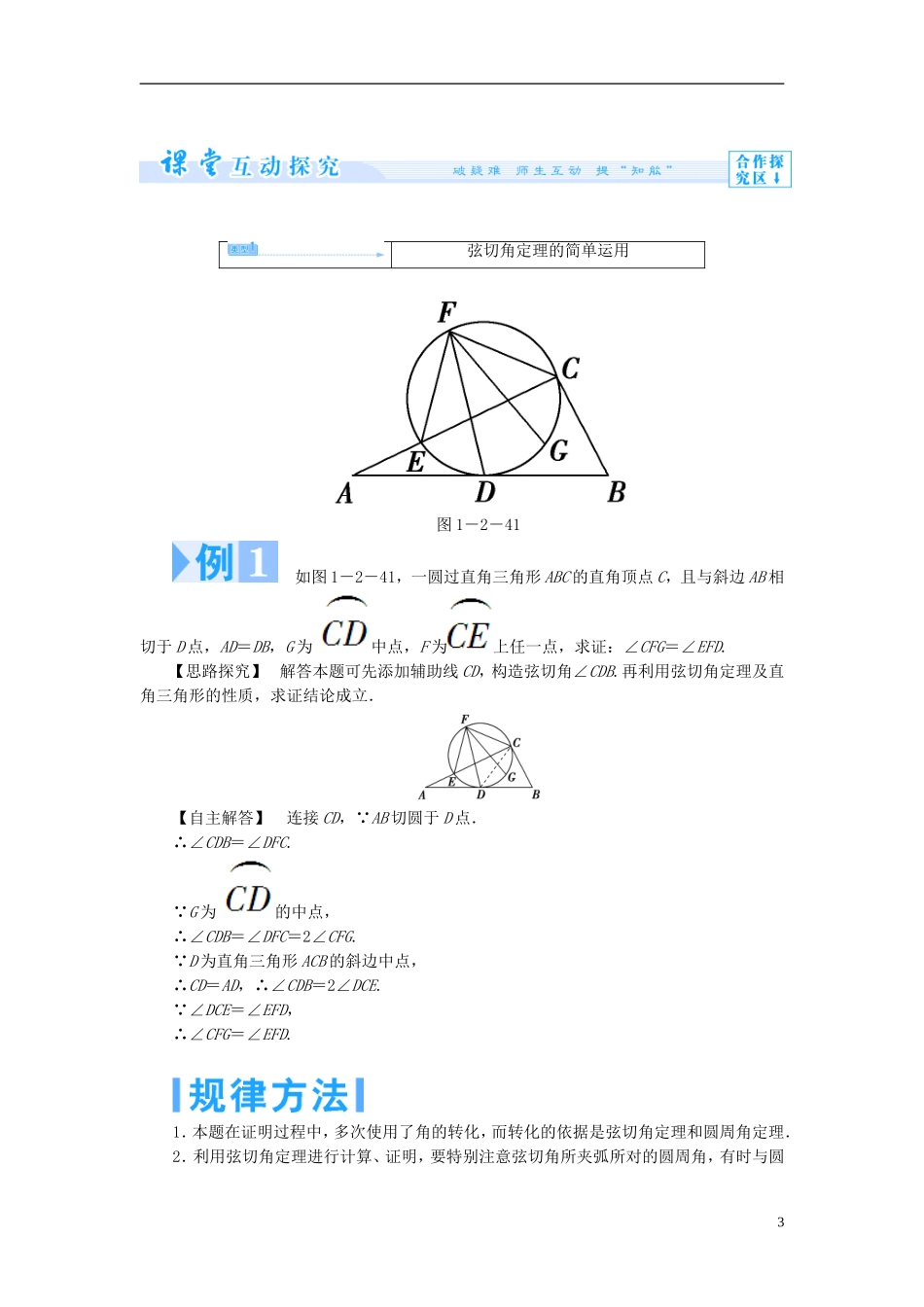
1.2.3 弦切角定理课标解读1.理解弦切角的定义.2.掌握弦切角定理,并能解决与弦切角有关的问题.3.体会分类思想、运动变化思想和化归思想.1.弦切角定义顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角.2.弦切角定理图 1-2-39(1)文字语言弦切角等于它所夹弧所对的圆周角;弦切角的度数等于它所夹弧的度数的一半.(2)图形语言如图 1-2-39,AB 与⊙O 切于 A 点,则∠BAC=∠ ADC .1.如图 1-2-40 所示,CE 是⊙O 的切线,切点为 C,你能说出弦切角∠BCE 与弦切角∠ACE 所夹的弧吗?1图 1-2-40【提示】 弦切角所夹的弧就是指构成弦切角的弦所对的夹在弦切角内部的一条弧,如图所示,弦切角∠BCE 所夹的弧是,弦切角∠ACE 所夹的弧是.2.如何正确使用弦切角定理?【提示】 要正确使用弦切角定理,第一步要找到弦切角,弦切角的特点是:(1)顶点在圆上;(2)一边与圆相交;(3)一边与圆相切,这三个条件缺一不可.第二步要准确地找到弦切角所夹的弧,再看这段弧上的圆周角,再用弦切角定理解题,如果没有圆周角,有这段弧所对的圆心角也行.2弦切角定理的简单运用图 1-2-41 如图 1-2-41,一圆过直角三角形 ABC 的直角顶点 C,且与斜边 AB 相切于 D 点,AD=DB,G 为中点,F 为上任一点,求证:∠CFG=∠EFD.【思路探究】 解答本题可先添加辅助线 CD,构造弦切角∠CDB.再利用弦切角定理及直角三角形的性质,求证结论成立.【自主解答】 连接 CD, AB 切圆于 D 点.∴∠CDB=∠DFC. G 为的中点,∴∠CDB=∠DFC=2∠CFG. D 为直角三角形 ACB 的斜边中点,∴CD=AD,∴∠CDB=2∠DCE. ∠DCE=∠EFD,∴∠CFG=∠EFD.1.本题在证明过程中,多次使用了角的转化,而转化的依据是弦切角定理和圆周角定理.2.利用弦切角定理进行计算、证明,要特别注意弦切角所夹弧所对的圆周角,有时与圆3的直径所对的圆周角结合运用,同时要注意根据题目的需要可添加辅助线构成所需要的弦切角. 图 1-2-42如图 1-2-42,⊙O 的弦 AB 的延长线和切线 EP 相交于点 P,E 为切点,∠APE 的平分线和 AE、BE 分别相交于 C、D.求证:EC=ED.【证明】 PE 切⊙O 于点 E,∴∠BEP=∠A, PC 平分∠APE,∴∠3=∠4,又 ∠1=∠3+∠A,∠2=∠4+∠BEP,∴∠1=∠2,∴EC=ED.弦切角定理的综合应用图 1-2-43 如 图 1 - 2 - 43 , PA 、 PB 是 ⊙ O 的 切 线 ...