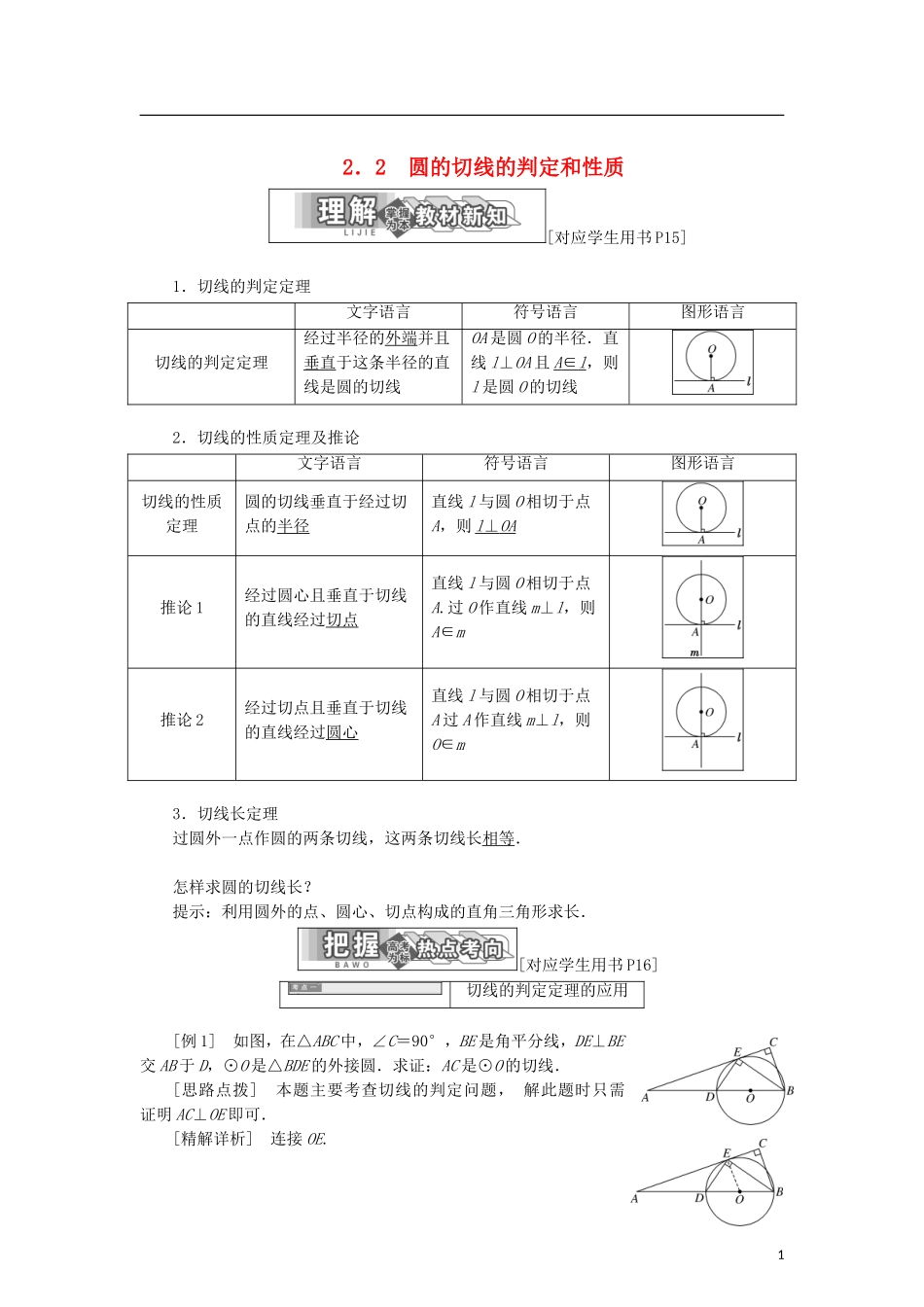
2.2 圆的切线的判定和性质[对应学生用书 P15]1.切线的判定定理文字语言符号语言图形语言切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线OA 是圆 O 的半径.直线 l⊥OA 且 A ∈ l ,则l 是圆 O 的切线2.切线的性质定理及推论文字语言符号语言图形语言切线的性质定理圆的切线垂直于经过切点的半径直线 l 与圆 O 相切于点A,则 l ⊥ OA 推论 1经过圆心且垂直于切线的直线经过切点直线 l 与圆 O 相切于点A.过 O 作直线 m⊥l,则A∈m推论 2经过切点且垂直于切线的直线经过圆心直线 l 与圆 O 相切于点A 过 A 作直线 m⊥l,则O∈m3.切线长定理过圆外一点作圆的两条切线,这两条切线长相等.怎样求圆的切线长?提示:利用圆外的点、圆心、切点构成的直角三角形求长.[对应学生用书 P16]切线的判定定理的应用[例 1] 如图,在△ABC 中,∠C=90°,BE 是角平分线,DE⊥BE交 AB 于 D,⊙O 是△BDE 的外接圆.求证:AC 是⊙O 的切线.[思路点拨] 本题主要考查切线的判定问题, 解此题时只需证明 AC⊥OE 即可.[精解详析] 连接 OE.1 OE=OB,∴∠OEB=∠OBE.又 BE 平分∠CBD,∴∠CBE=∠DBE.∴∠OEB=∠CBE.∴EO∥CB. ∠C=90°,∴∠AEO=90°,即 AC⊥OE. E 为⊙O 半径 OE 的外端,∴AC 是⊙O 的切线.证明直线与圆相切一般有以下几种方法:(1)直线与圆只有一个公共点;(2)圆心到直线的距离等于圆的半径;(3)切线的判定定理.几何证明问题常用方法(3).1.如图,AB 是⊙O 的直径,BC 交⊙O 于点 D,DE⊥AC 于点 E,要使 DE 是⊙O 的切线,还需补充一个条件,则补充的条件不正确的是( )A.DE=DO B.AB=ACC.CD=DB D.AC∥OD解析:选 A 当 AB=AC 时,如图:连接 AD,因为 AB 是⊙O 的直径,所以 AD⊥BC,所以 CD=BD,因为 AO=BO,所以 OD 是△ABC 的中位线,所以 OD∥AC,因为 DE⊥AC,所以 DE⊥OD,所以 DE 是⊙O 的切线.所以 B 正确.当 CD=BD 时,AO=BO,同 B,所以 C 正确.当 AC∥OD 时,因为 DE⊥AC,2所以 DE⊥OD.所以 DE 是⊙O 的切线.所以 D 正确.2.已知 D 是△ABC 的边 AC 上的一点,AD∶DC=2∶1,∠C=45°,∠ADB=60°,求证:AB是△BCD 的外接圆的切线.证明:如图,连接 OB,OC,OD,OD 交 BC 于 E. ∠DCB 是 BD 所对的圆周角,∠BOD 是 BD 所对的圆心角,∠...