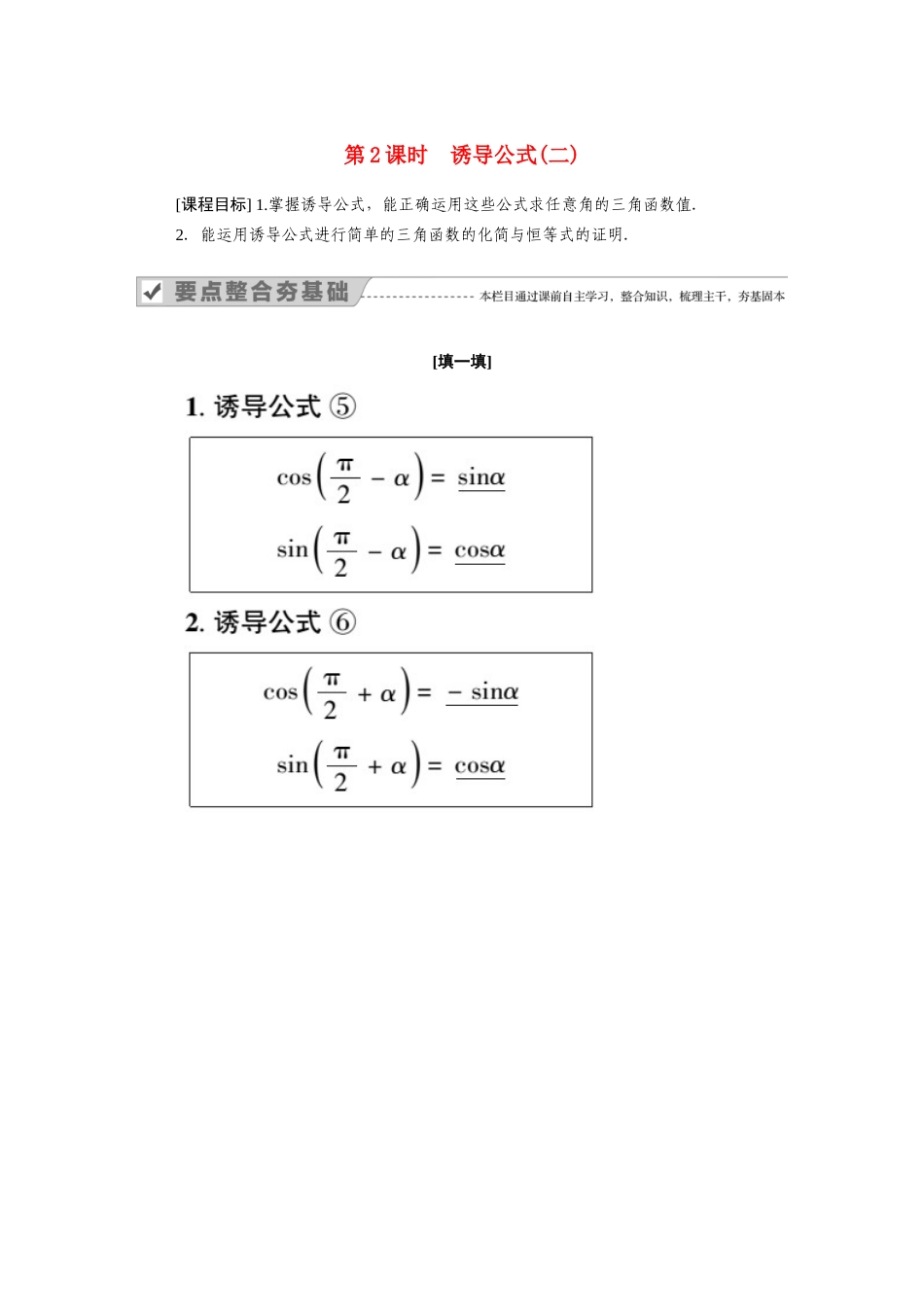
第 2 课时 诱导公式(二)[课程目标] 1.掌握诱导公式,能正确运用这些公式求任意角的三角函数值.2.能运用诱导公式进行简单的三角函数的化简与恒等式的证明.[填一填][答一答]1.角 α 与-α 以及角 α 与+α 间三角函数关系是如何推导的?提示:(1)如图,设任意角 α 的终边与单位圆的交点 P1的坐标为(x,y),由于角-α 的终边与角 α 的终边关于直线 y=x 对称,角-α 的终边与单位圆的交点 P2与 P1关于直线 y=x 对称,因此点 P2的坐标是(y,x),于是有:cosα=x,sinα=y;cos=y,sin=x,从而有 sin=cosα,cos=sinα.(2) +α=-(-α),∴sin=sin=cos(-α)=cosα,cos=cos=sin(-α)=-sinα.即 sin=cosα,cos=-sinα.2.如何快速记忆所学的诱导公式?提示:(1)±α、±α 的三角函数等于 α 的余函数,前边放上把 α 看作锐角时,该角所在象限的原函数值的符号.即“函数变余函,符号看象限”.(2)诱导公式可并在一起记忆如下:2kπ±α(k∈Z) , π±α , - α , ±α , ±α , (2k + 1)π±α(k∈Z) 的 三 角 函 数 , 可 以 统 记 作±α(k∈Z).±α 的三角函数,当 k 为偶数时,等于角 α 的同名函数,前边放上把 α 看作锐角时,该角所在象限的原函数值的符号;当 k 为奇数时,等于角 α 的余函数,前边放上把角 α 看作锐角时,该角所在象限的原函数值的符号,即“奇变偶不变,符号看象限”.类型一 给角求值[例 1] 求下列各三角函数值.(1)sin(-1 920°);(2)cos(-1 560°);(3)tan.[分析] 应用诱导公式来化简求值.[解] (1)原式=-sin1 920°=-sin(360°×5+120°)=-sin(90°+30°)=-cos30°=-;(2)原式=cos1 560°=cos(360°×4+120°)=cos120°=cos(90°+30°)=-sin30°=-;(3)原式=tan=tan=1.[变式训练 1] 求下列各三角函数值:(1)sin;(2)cosπ;(3)sinπ.解:(1)sin=-sin=-sin=-sin=-sin=sin=.(2)cosπ=cos=cos=cos=-cos=-.(3)sin=sin=sin=sin=cos=.类型二 给值求值[例 2] 已知 sin=,求 cos 的值.[分析] 尝试对角进行整体分析的方法,建立互余或互补角关系的思想,然后套用诱导公式解决.[解] sin=,且+=,∴cos=cos=sin=.[变式训练 2] (1)已知 cos(π+α)=-,α 为第一象限角,求 cos 的值;(2)已知 cos=,求 cos·sin 的值...