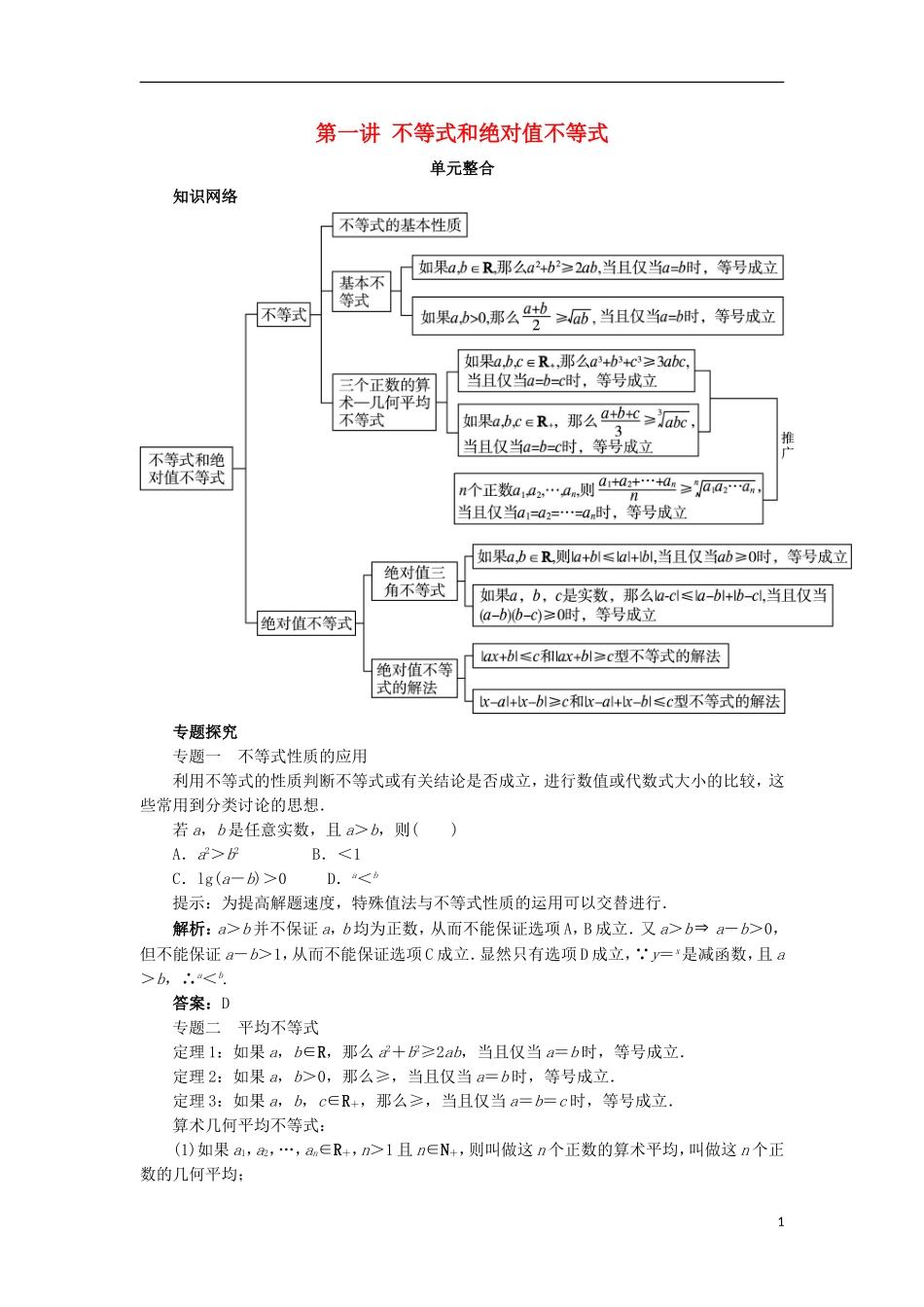
第一讲 不等式和绝对值不等式单元整合知识网络专题探究专题一 不等式性质的应用利用不等式的性质判断不等式或有关结论是否成立,进行数值或代数式大小的比较,这些常用到分类讨论的思想.若 a,b 是任意实数,且 a>b,则( )A.a2>b2 B.<1C.lg(a-b)>0 D.a<b提示:为提高解题速度,特殊值法与不等式性质的运用可以交替进行.解析:a>b 并不保证 a,b 均为正数,从而不能保证选项 A,B 成立.又 a>b a-b>0,但不能保证 a-b>1,从而不能保证选项 C 成立.显然只有选项 D 成立, y=x是减函数,且 a>b,∴a<b.答案:D专题二 平均不等式定理 1:如果 a,b∈R,那么 a2+b2≥2ab,当且仅当 a=b 时,等号成立.定理 2:如果 a,b>0,那么≥,当且仅当 a=b 时,等号成立.定理 3:如果 a,b,c∈R+,那么≥,当且仅当 a=b=c 时,等号成立.算术几何平均不等式:(1)如果 a1,a2,…,an∈R+,n>1 且 n∈N+,则叫做这 n 个正数的算术平均,叫做这 n 个正数的几何平均;1(2)推广到一般情形:对于 n 个正数 a1,a2,…,an,它们的算术平均不小于它们的几何平均,即≥,当且仅当 a1=a2=…=an时,等号成立.语言表述:n 个正数的算术平均不小于它们的几何平均.(3)≥的几何解释:如图,以 a+b 为直径作圆,在直径 AB 上取一点 C,过 C 作弦 DD′⊥AB 交 AB 于 C,则 CD2=CA·CB=ab,从而 CD=,则半径≥CD=.若 x , y > 0 , 设 Q(x , y) = , A(x , y) = , G(x , y) = , H(x , y) = , 求 证 :Q (x,y)≥A(x,y)≥ G(x,y)≥H(x,y).证明: 2=≤=,∴≥,即 Q(x,y)≥A(x,y).由基本不等式,得 A(x,y)≥G(x,y).H(x,y)=≤==G(x,y),即 G(x,y)≥H(x,y).综上所述:Q(x,y)≥A(x,y)≥G(x,y)≥H(x,y).专题三 利用平均不等式求最大(小)值重要的结论:已知 x,y 都是正实数,则:(1)如果积 xy 是定值 P,那么当 x=y 时,和 x+y 有最小值 2;(2)如果和 x+y 是定值 S,那么当 x=y 时,积 xy 有最大值 S2.求函数 y=2x2+(x>0)的最小值.下列解法是否正确?为什么?解法一:y=2x2+=2x2++≥3=3,∴ymin=3.解法二:y=2x2+≥2=2,当且仅当 2x2=,即 x=时,ymin=2=2=2.解:题目中两种解法均有错误.解法一错在等号不成立,即不存在 x,使得 2x2==;解...