高中数学 第一章 集合与函数 习题课 集合学案（含解析）新人教A版必修1-新人教A版高一必修1数学学案

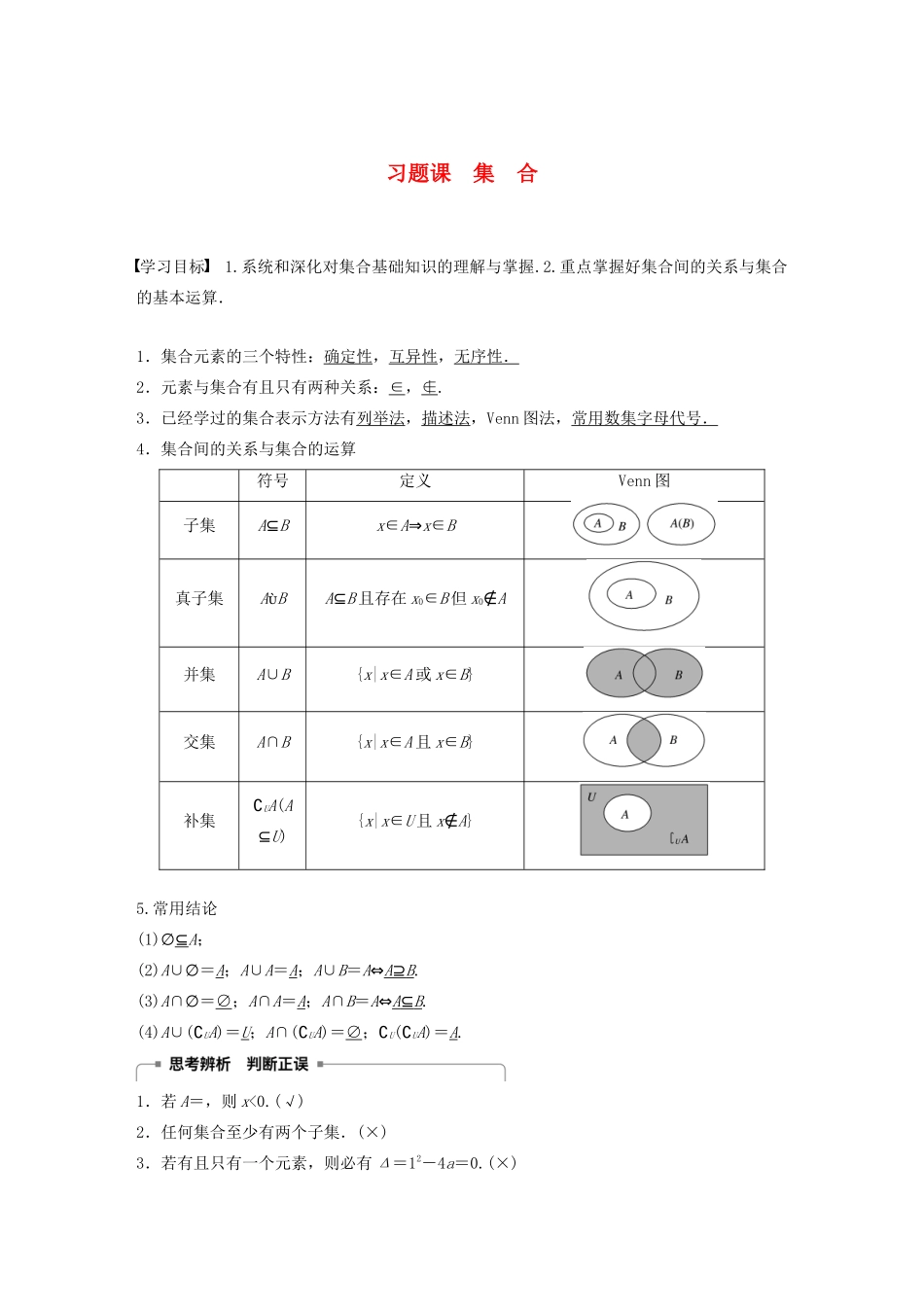
习题课 集 合学习目标 1.系统和深化对集合基础知识的理解与掌握.2.重点掌握好集合间的关系与集合的基本运算．1．集合元素的三个特性：确定性，互异性，无序性．2．元素与集合有且只有两种关系：∈，∉.3．已经学过的集合表示方法有列举法，描述法，Venn 图法，常用数集字母代号．4．集合间的关系与集合的运算符号定义Venn 图子集A⊆Bx∈A⇒x∈B真子集ABA⊆B 且存在 x0∈B 但 x0∉A并集A∪B{x|x∈A 或 x∈B}交集A∩B{x|x∈A 且 x∈B}补集∁UA(A⊆U){x|x∈U 且 x∉A}5.常用结论(1)∅⊆A；(2)A∪∅＝A；A∪A＝A；A∪B＝A⇔A ⊇ B .(3)A∩∅＝∅；A∩A＝A；A∩B＝A⇔A ⊆ B .(4)A∪(∁UA)＝U；A∩(∁UA)＝∅；∁U(∁UA)＝A.1．若 A＝，则 x<0.(√)2．任何集合至少有两个子集．(×)3．若有且只有一个元素，则必有 Δ＝12－4a＝0.(×)4．设 A，B 为全集的子集，则 A∩B＝A⇔A∪B＝B⇔∁UA⊇∁UB.(√)类型一 集合的概念及表示法例 1 下列表示同一集合的是( )A．M＝{(2,1)，(3,2)}，N＝{(1,2)}B．M＝{2,1}，N＝{1,2}C．M＝{y|y＝x2＋1，x∈R}，N＝{y|y＝x2＋1，x∈N}D．M＝{(x，y)|y＝x2－1，x∈R}，N＝{y|y＝x2－1，x∈R}考点 集合的表示综合题点 集合的表示综合问题答案 B解析 A 中 M，N 两集合的元素个数不同，故不可能相同；B 中 M，N 均为含有 1,2 两个元素的集合，由集合中元素的无序性可得 M＝N；C 中 M，N 均为数集，显然有 MN；D 中 M 为点集，即抛物线 y＝x2－1 上所有点的集合，而 N 为数集，即抛物线 y＝x2－1 的 y 的取值，故选 B.反思与感悟 要解决集合的概念问题，必须先弄清集合中元素的性质，明确是数集，还是点集等．跟踪训练 1 设集合 A＝{(x，y)|x－y＝0}，B＝{(x，y)|2x－3y＋4＝0}，则 A∩B＝________.考点 交集的概念及运算题点 无限集合的交集运算答案 {(4,4)}解析 由得∴A∩B＝{(4,4)}．类型二 集合间的基本关系例 2 若集合 P＝{x|x2＋x－6＝0}，S＝{x|ax＋1＝0}，且 S⊆P，求由 a 的可能取值组成的集合．考点 子集及其运算题点 根据子集关系求参数的取值范围解 由题意得，P＝{－3,2}．当 a＝0 时，S＝∅，满足 S⊆P；当 a≠0 时，方程 ax＋1＝0 的解为 x＝－，为满足 S⊆P，可使－＝－3，或－＝2，即 a＝，或 a＝－.故所求集合为.反思与感悟 (1)在分类时要遵循“不重不漏”的原则，然后对于每一类情况都要给出问题的解答．(2)...