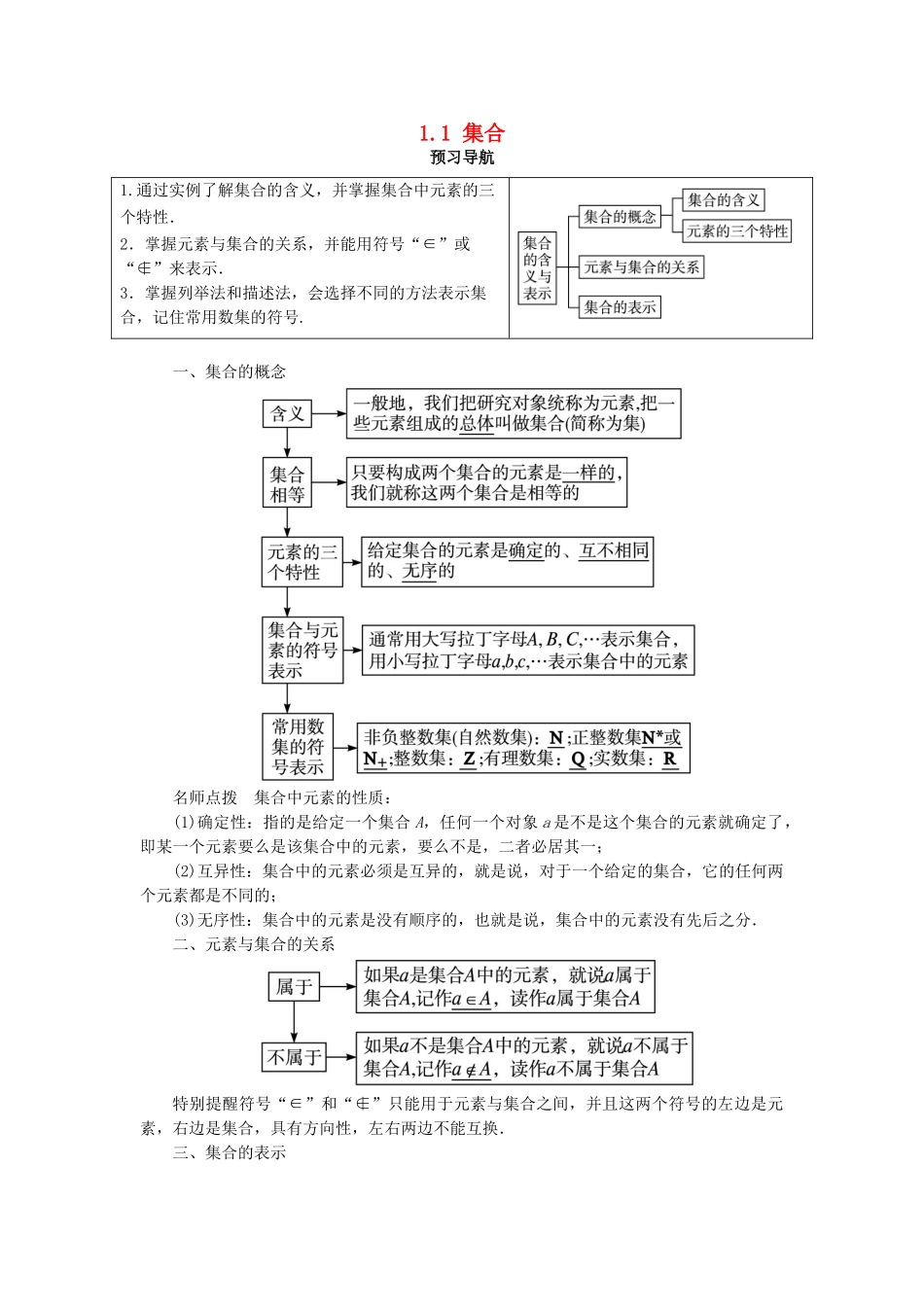
1.1 集合预习导航1.通过实例了解集合的含义,并掌握集合中元素的三个特性.2.掌握元素与集合的关系,并能用符号“∈”或“∉”来表示.3.掌握列举法和描述法,会选择不同的方法表示集合,记住常用数集的符号.一、集合的概念名师点拨 集合中元素的性质:(1)确定性:指的是给定一个集合 A,任何一个对象 a 是不是这个集合的元素就确定了,即某一个元素要么是该集合中的元素,要么不是,二者必居其一;(2)互异性:集合中的元素必须是互异的,就是说,对于一个给定的集合,它的任何两个元素都是不同的;(3)无序性:集合中的元素是没有顺序的,也就是说,集合中的元素没有先后之分.二、元素与集合的关系特别提醒符号“∈”和“∉”只能用于元素与集合之间,并且这两个符号的左边是元素,右边是集合,具有方向性,左右两边不能互换.三、集合的表示自主思考 1 什么样的集合可以用列举法来表示?提示:对于元素个数很少或元素存在明显规律的集合可用列举法表示.自主思考 2 在描述法中,表示这个集合元素的一般符号不同,但竖线后的条件一样 ,那么这样的集合还相同吗?如 A={x|y=},B={(x,y)|y=}.提示:一般地,这样两个集合是不相同的,如集合 A={x|y=}表示集合{x|x≥1},而集合 B={(x,y)|y=}表示二元方程 y=的解组成的集合或是函数y=图象上所有点组成的集合.自主思考 3 用列举法与描述法表示集合的区别是什么?提示:列举法描述法一般形式{a1,a2,a3,…,an}{x∈I|p(x)}适用范围有限集或规律性较强的无限集有限集、无限集均可特点直观、明了抽象、概括