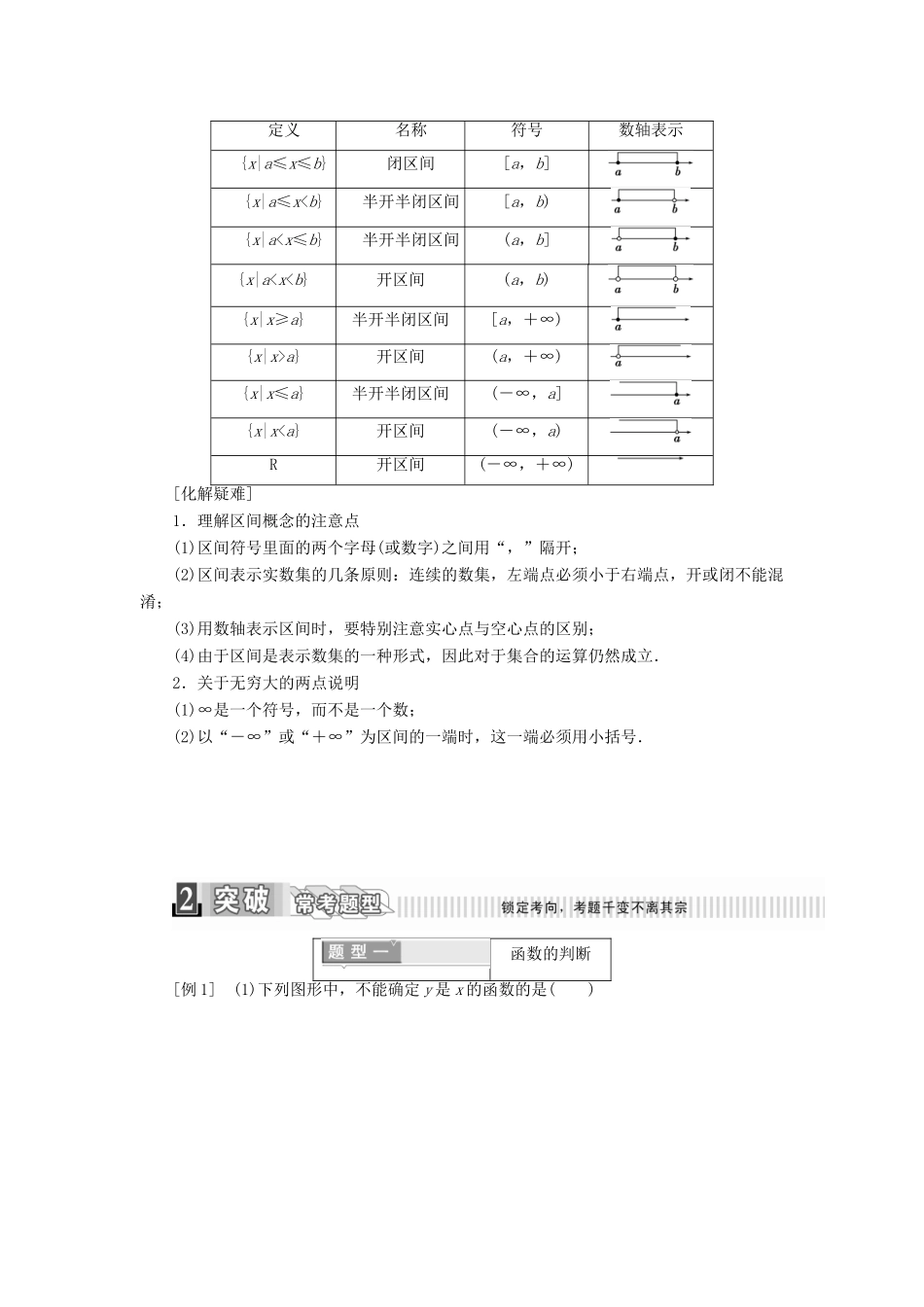
1.2.1 函数的概念函数的概念[提出问题]某物体从高度为 44.1 m 的空中自由下落,物体下落的距离 s(m)与所用时间 t(s)的平方成正比,这个规律用数学式子可以描述为 s=gt2,其中 g 取 9.8 m/s2.问题 1:时间 t 和物体下落的距离 s 有何限制?提示:0≤t≤3,0≤s≤44.1.问题 2:时间 t(0≤t≤3)确定后,下落的距离 s 确定吗?提示:确定.问题 3:下落后的某一时刻,能同时对应两个距离吗?提示:不能.[导入新知]函数的有关概念函数的概念设 A,B 是非空的数集,如果按照某种对应关系 f,使对于集合 A 中任意一个数 x ,在集合 B 中都有唯一确定的数 f ( x ) 和它对应,那么就称 f : A → B 为从集合 A 到集合 B 的一个函数函数的记法y = f ( x ) , x ∈ A 定义域x 叫做自变量,x 的取值范围 A 叫做函数的定义域值域函数值的集合{ f ( x )| x ∈ A } 叫做函数的值域[化解疑难]理解函数的概念应关注五点(1)“A,B 是非空的数集”,一方面强调了 A,B 只能是数集,即 A,B 中的元素只能是实数;另一方面指出了定义域、值域都不能是空集,也就是说定义域为空集的函数是不存在的.(2)理解函数的概念要注意,函数的定义域是非空数集 A,但函数的值域不一定是非空数集 B,而是集合 B 的子集.(3)函数定义中强调“三性”:任意性、存在性、唯一性,即对于非空数集 A 中的任意一个(任意性)元素 x,在非空数集 B 中都有(存在性)唯一(唯一性)的元素 y 与之对应.这三性只要有一个不满足,便不能构成函数.(4)y=f(x)仅仅是函数符号,不是表示“y 等于 f 与 x 的乘积”,f(x)也不一定就是解析式.(5)除 f(x)外,有时还用 g(x),u(x),F(x),G(x)等符号来表示函数.区 间[导入新知]区间的概念及表示定义名称符号数轴表示{x|a≤x≤b}闭区间[a,b]{x|a≤x
a}开区间(a,+∞){x|x≤a}半开半闭区间(-∞,a]{x|x