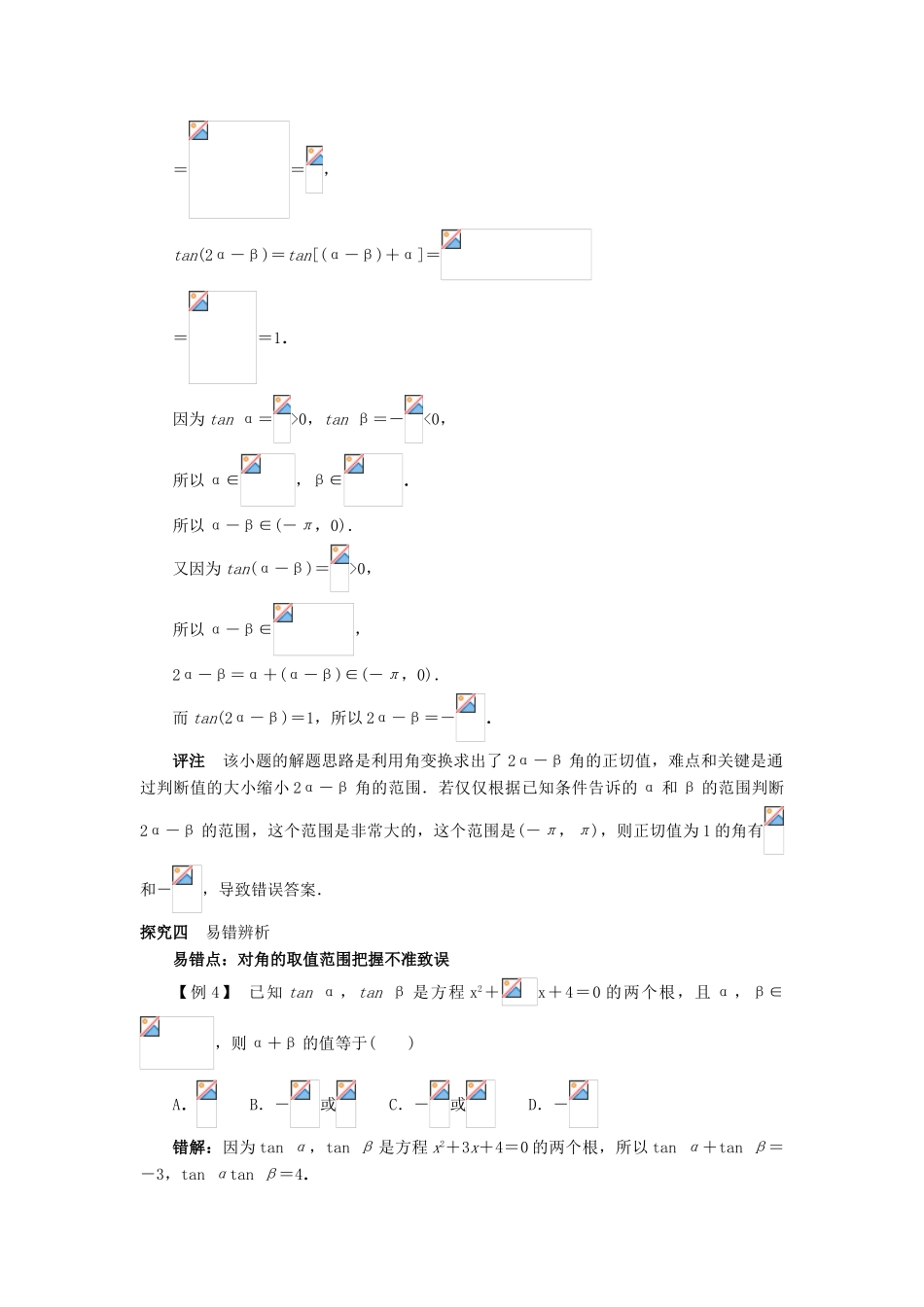
3.1.3 两角和与差的正切课堂探究探究一 利用和(差)角正切公式求值对于形如:的式子,常常分子、分母同时除以 cos α转化为的形式,再化为的形式,逆用公式 Tα+β即可.【例 1】 计算:(1) ;(2) ;(3)tan 15°+tan 30°+tan 15°tan 30°.分析:由两角和与差公式 Tα±β的特点易知(1)(2)可逆用公式 Tα±β,而(3)应使用公式Tα+β的变形.解:(1)解法一:tan 75°=tan(45°+30°)=====2+.所以===-=-.解法二:==tan(45°+75°)=tan 120°=-tan 60°=-.(2) ====tan (45°-15°)=tan 30°=.(3)公式 tan(α+β)=可变形为tan α+tan β=tan(α+β)(1-tan αtan β),所以 tan 15°+tan 30°+tan 15°tan 30°=tan 45°(1-tan 15°tan 30°)+tan 15°tan 30°=tan 45°=1.探究二 给值求值问题若所求三角函数的角可用已知三角函数的角的和或差表示就可求出其值,即角变换思想同样可以运用到和差角的正切公式上求值.【例 2】 已知 tan(α+β)=5,tan(α-β)=3,求 tan 2α,tan 2β,tan的值.解:tan 2α=tan[(α+β)+(α-β)]===-.tan 2β=tan[(α+β)-(α-β)]===.tan===.探究三 给值求角问题【例 3】 已知 tan(α-β)=,tan β=-,α,β∈(0,π),求 2α-β 的值.分析:已知 α-β 及 β 角的正切,要求 2α-β 的正切,必须通过角变换,2α-β=α+(α-β),α=(α-β)+β,故需先求出 α 角的正切.解:因为 tan β=-,tan(α-β)=,所以 tan α=tan[(α-β)+β]===,tan(2α-β)=tan[(α-β)+α]===1.因为 tan α=>0,tan β=-<0,所以 α∈,β∈.所以 α-β∈(-π,0).又因为 tan(α-β)=>0,所以 α-β∈,2α-β=α+(α-β)∈(-π,0).而 tan(2α-β)=1,所以 2α-β=-.评注 该小题的解题思路是利用角变换求出了 2α-β 角的正切值,难点和关键是通过判断值的大小缩小 2α-β 角的范围.若仅仅根据已知条件告诉的 α 和 β 的范围判断2α-β 的范围,这个范围是非常大的,这个范围是(-π,π),则正切值为 1 的角有和-,导致错误答案.探究四 易错辨析易错点:对角的取值范围把握不准致误【例 4】 已知 tan α,tan β 是方程 x2+x+4=0 的两个根,且 α,β∈,则 α+β 的值等于( ...