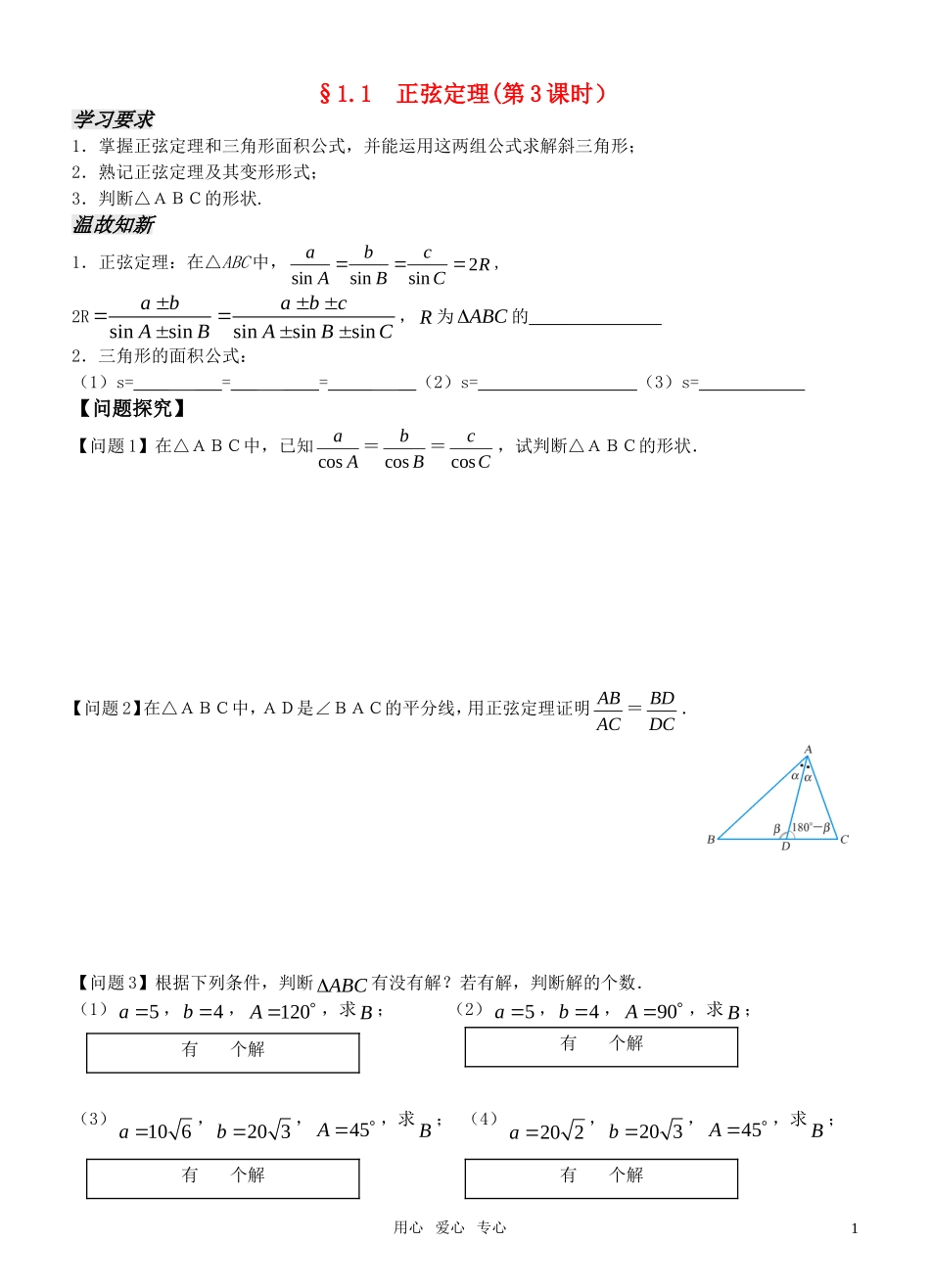
§1.1 正弦定理(第 3 课时)学习要求 1.掌握正弦定理和三角形面积公式,并能运用这两组公式求解斜三角形;2.熟记正弦定理及其变形形式;3.判断△ABC的形状.温故知新1.正弦定理:在△ABC 中,CcBbAasinsinsinR2,2RsinsinsinsinsinababcABABC , R 为 ABC的_______________2.三角形的面积公式:(1)s=____ ___=___ ____=_____ __(2)s=__________________(3)s=____________【问题探究】【问题 1】在△ABC中,已知Aacos=Bbcos=Cccos,试判断△ABC的形状.【问题 2】在△ABC中,AD是∠BAC的平分线,用正弦定理证明ACAB =DCBD .【问题 3】根据下列条件,判断 ABC有没有解?若有解,判断解的个数.(1)5a ,4b ,120A ,求 B ; (2)5a ,4b ,90A ,求 B ;(3)10 6a ,20 3b ,45A ,求 B ; (4)20 2a ,20 3b ,45A ,求 B ;用心 爱心 专心1有 个解有 个解有 个解有 个解(5)4a ,10 33b ,60A ,求 B .巩固提高1. 在△ABC 中,若BA2,则a 等于 ( )A.Absin2 B.Abcos2 C.Bbsin2 D.Bbcos22. 在△ABC 中,若22tantanbaBA ,则△ABC 的形状是 ( )A.直角三角形 B.等腰或直角三角形 C.不能确定 D.等腰三角形3.在 ABC中,::4:1:1A B C ,则: :a b c ( )A.4:1:1 B.2:1:1 C.2 :1:1 D. 3 :1:14.已知△ABC 中,a∶b∶c=1∶3 ∶2,则 A∶B∶C 等于 ( )A.1∶2∶3 B.2∶3∶1 C.1∶3∶2 D.3∶1∶25.在 ABC中,若sin:sin:sin4:5:6ABC ,且15abc ,则a ,b ,c .6.在△ABC 中,证明:2222112cos2cosbabBaA【拓展延伸】7.如图所示,在等边三角形中,,ABaO为三角形的中心,过O的直线交AB于M ,交 AC 于 N ,求2211OMON的最大值和最小值..用心 爱心 专心2有 个解