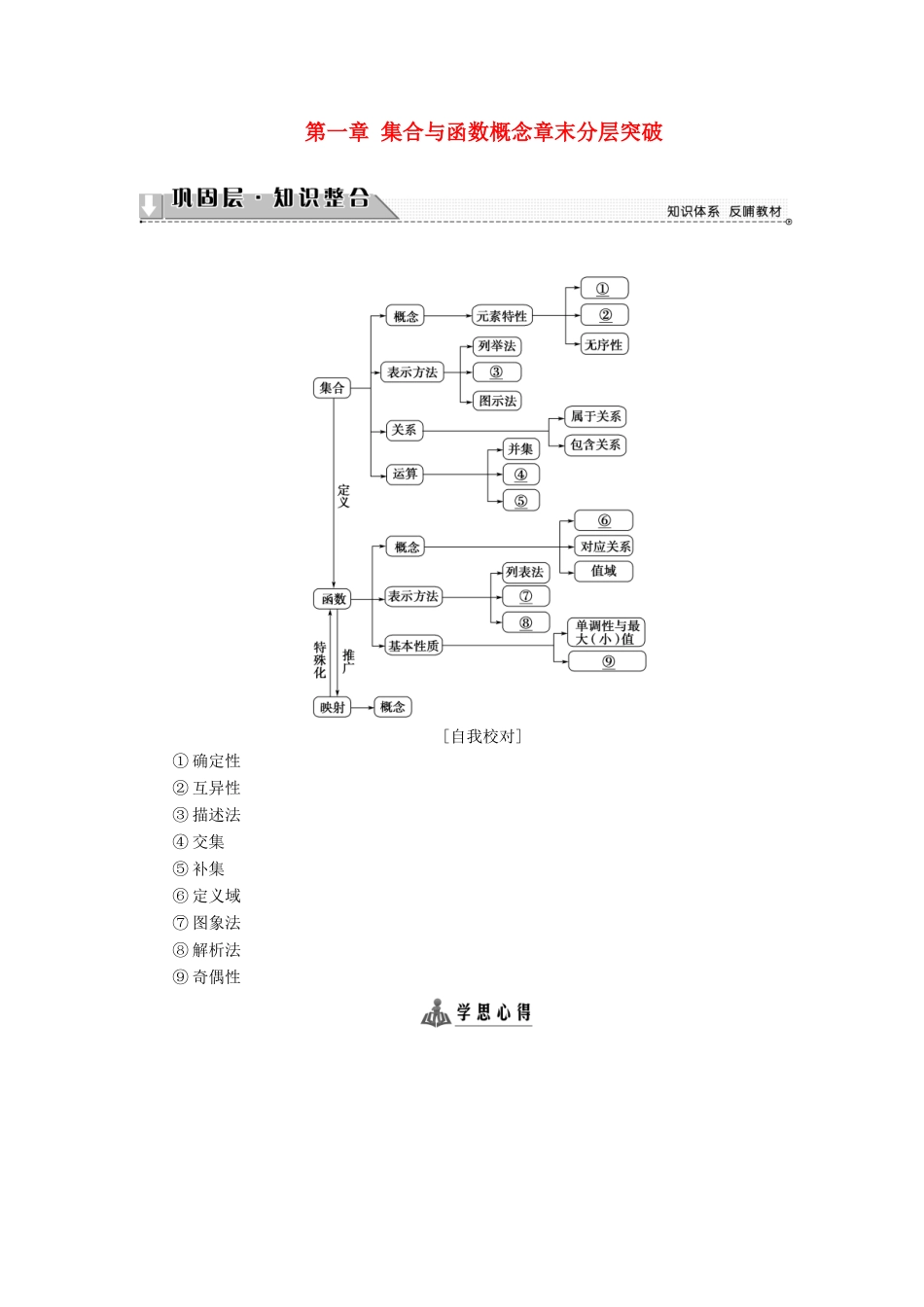
第一章 集合与函数概念章末分层突破 [自我校对]① 确定性② 互异性③ 描述法④ 交集⑤ 补集⑥ 定义域⑦ 图象法⑧ 解析法⑨ 奇偶性集合的运算集合的运算是指集合间的交、并、补集三种常见的运算.若集合中的元素是离散的,集合的运算一般运用定义或韦恩图;若集合中的元素是连续的(如用不等式表示的),则用数轴法;特别地,若集合中含有参数,有时需要对参数进行讨论. 已知全集为 U=R,集合 A={x|-1<x<2},B={x|0<x<3},M={x|2x-a<0}.(1)求 A∩(∁UB);(2)若(A∪B)⊆M,求实数 a 的取值范围.【精彩点拨】 (1)利用数轴,根据集合的基本运算即可求 A∩(∁UB);(2)根据(A∪B)⊆M,建立条件关系即可求实数 a 的取值范围.【规范解答】 (1)因为 A={x|-1<x<2},B={x|0<x<3},所以∁UB={x|x≥3 或x≤0},则 A∩(∁UB)={x|-1<x≤0}.(2)A∪B={x|-1<x<3},M={x|2x-a<0}=,若(A∪B)⊆M,则≥3,解得 a≥6,则实数 a 的取值范围[6,+∞).[再练一题]1.已知集合 A={x|x2-5x+6=0},B={x|x2+ax+6=0}且 B⊆A,求实数 a 的取值范围. 【导学号:97030067】【解】 集合 A={x|x2-5x+6=0}={2,3},且 B⊆A,∴B=∅,或 B={2},或 B={3},或 B={2,3},若 B=∅,则 Δ=a2-24<0,解得 a∈(-2,2),若 B={2},B 中方程的常数项为 4≠6,故不存在满足条件的 a 值;若 B={3},B 中方程的常数项为 9≠6,故不存在满足条件的 a 值;若 B={2,3},则 a=-5,综上,实数 a 的取值范围为{-5}∪(-2,2).函数的概念函数有三要素:定义域、值域和对应关系,其中定义域是研究函数问题的前提条件,研究函数的性质首先要注意函数的定义域,而求函数的解析式、值域(最值)问题是高考的重点、热点. (1)函数 y=+(2x+1)0的定义域是________.(2)设集合 A=,B=,函数 f(x)=若 x0∈A,且 f(f(x0))∈A,则 x0 的取值范围是( )A. B.C. D.【精彩点拨】 (1)根据函数的解析式,列出使函数有意义的不等式组,求出解集即可.(2)先由 x0∈A 计算 f(x0)的值,依据 f(x0)的范围计算 f(f(x0)),由 0≤f(f(x0))<求 x0的取值范围.【规范解答】 (1) 函数 y=+(2x+1)0,∴解得 x<,且 x≠-,∴函数的定义域是.(2) x0∈A,∴f(x0)=x0+∈B,∴f(f(x0))=f=2,即 f(f(x0))=1-2x0∈A,∴0≤1-2x0<,即