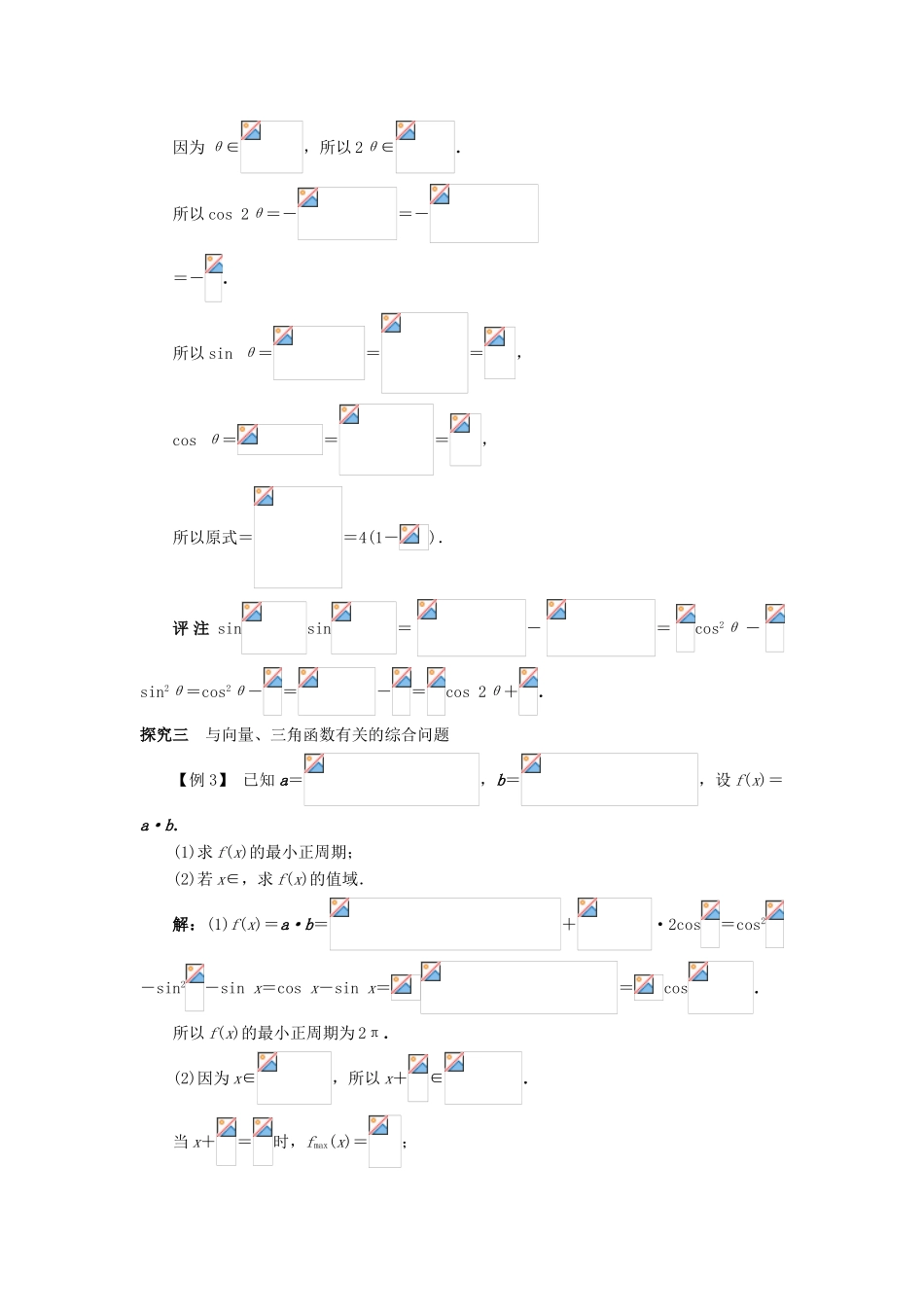
3.2.2 半角的正弦余弦和正切课堂探究探究一 利用半角公式化简求值问题对于化简求值问题要遵循三个“统一”,即统一角,统一函数名称,统一结构形式,另外还要有必要的切化弦、通分、角变换等常用技巧.【例 1】 (1)求值:(tan 5°-cot 5°)·;(2)已知 sin-cos=-,<α<π,求 tan的值.解:(1)原式=·=·=-2··=-2cot 10°·tan 10°=-2.(2)因为=,所以 1-sin α=,所以 sin α=.又因为<α<π,所以 cos α=-.所以 tan===2.探究二 给值求值问题【例 2】 已知 tan 2θ=-2,θ∈,求的值.分析:先化简,再求值.解:原式=.因为 θ∈,所以 2θ∈.所以 cos 2θ=-=-=-.所以 sin θ===,cos θ===,所以原式==4(1-).评 注 sinsin=-=cos2θ -sin2θ=cos2θ-=-=cos 2θ+.探究三 与向量、三角函数有关的综合问题【例 3】 已知 a=,b=,设 f(x)=a·b.(1)求 f(x)的最小正周期;(2)若 x∈,求 f(x)的值域.解:(1)f(x)=a·b=+·2cos=cos2-sin2-sin x=cos x-sin x==cos.所以 f(x)的最小正周期为 2π.(2)因为 x∈,所以 x+∈.当 x+=时,fmax(x)=;当 x+=π 时,fmin(x)=-.故 f(x)的值域为.探究四 易错辨析易错点:没有分类讨论而漏解【例 4】 在等腰三角形中,已知顶角 θ 的正弦值为,试求该三角形底角的正弦值、余弦值和正切值.错解:因为 sin θ=,所以 cos θ=.设等腰三角形的底角为 α,则 2α+θ=π,即 α=-,所以 sin α=sin=cos=±=±,cos α=cos=sin=±=±,所以 tan α==±3.错因分析:错误一是由 sin θ=求 cos θ 没有分类讨论;错误二是由 cos θ 求 α的正弦值、余弦值和正切值时没有检验符号.正解:设等腰三角形的底角为 α,则 2α+θ=π,即 α=-.由 sin θ=,得 cos θ=±.① 当 cos θ=时,sin α=cos==,cos α=sin==.所以 tan α==3.② 当 cos θ=-时,sin α=cos==,cos α=sin==,所以 tan α==.