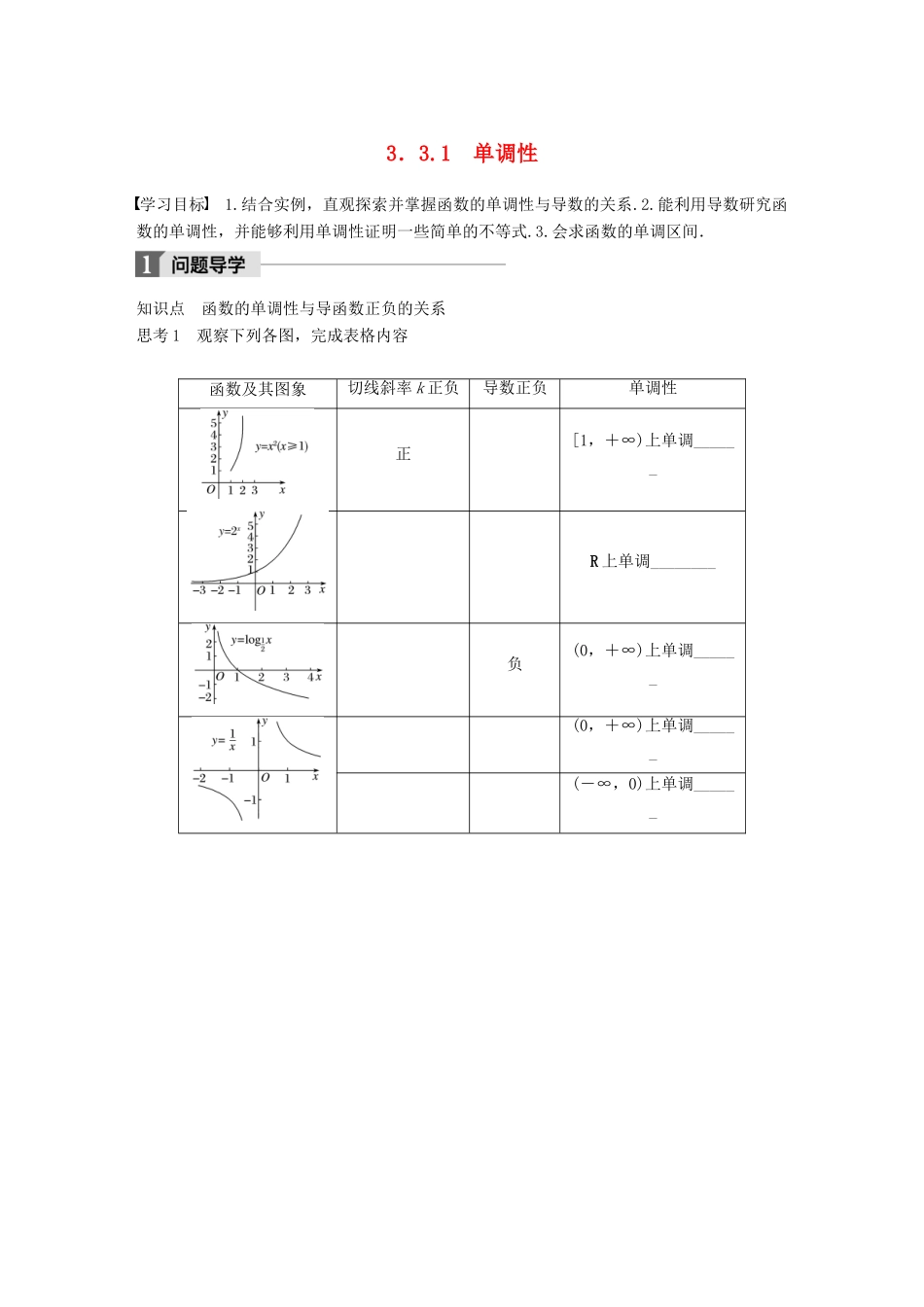
3.3.1 单调性学习目标 1.结合实例,直观探索并掌握函数的单调性与导数的关系.2.能利用导数研究函数的单调性,并能够利用单调性证明一些简单的不等式.3.会求函数的单调区间.知识点 函数的单调性与导函数正负的关系思考 1 观察下列各图,完成表格内容函数及其图象切线斜率 k 正负导数正负单调性正[1,+∞)上单调______R 上单调________负(0,+∞)上单调______(0,+∞)上单调______(-∞,0)上单调______思考 2 依据上述分析,可得出什么结论? 梳理 (1)导数值切线的斜率倾斜角曲线的变化趋势函数的单调性>0________0______角单调______<0________0______角单调______(2)在区间(a,b)内函数的单调性与导数有如下关系:函数的单调性导数单调递________f′(x) ≥0,且 f′(x)在(a,b)的任何子区间上都不恒为零单调递________f′(x)≤0,且 f′(x)在(a,b)的任何子区间上都不恒为零常函数f′(x)=0类型一 求函数的单调区间命题角度 1 求不含参数的函数的单调区间例 1 求 f(x)=3x2-2ln x 的单调区间. 反思与感悟 求函数 y=f(x)的单调区间的步骤(1)确定函数 y=f(x)的定义域;(2)求导数 y′=f′(x);(3)解不等式 f′(x)>0,函数在定义域内的解集上为增函数;(4)解不等式 f′(x)<0,函数在定义域内的解集上为减函数.跟踪训练 1 求函数 f(x)=的单调区间. 命题角度 2 求含参数的函数的单调区间例 2 讨论函数 f(x)=x2-aln x(a≥0)的单调性.引申探究若将本例改为 f(x)=ax2-ln x(a∈R)呢? 反思与感悟 (1)在判断含有参数的函数的单调性时,不仅要考虑到参数的取值范围,而且要结合函数的定义域来确定 f′(x)的符号,否则会产生错误.(2)分类讨论是把整个问题划分为若干个局部问题,在每一个局部问题中,原先的不确定因素就变成了确定性因素,当这些局部问题都解决了,整个问题就解决了.跟踪训练 2 已知函数 f(x)=4x3+3tx2-6t2x+t-1,其中 x∈R,t∈R.当 t≠0 时,求f(x)的单调区间. 类型二 证明函数的单调性问题例 3 证明:函数 f(x)=在区间上单调递减. 反思与感悟 关于利用导数证明函数单调性的问题:(1)首先考虑函数的定义域,所有函数性质的研究必须保证在定义域内这个前提下进行.(2)f′(x)>(或<)0,则 f(x)为单调递增(或递减)函数;但要特别注意,f(x)为单调递增(或递减)函数,则 f′(x)≥(或≤)0.跟踪训练 3 证明:函数 f(x)=在区间(0,e)上是增函数. 类型...