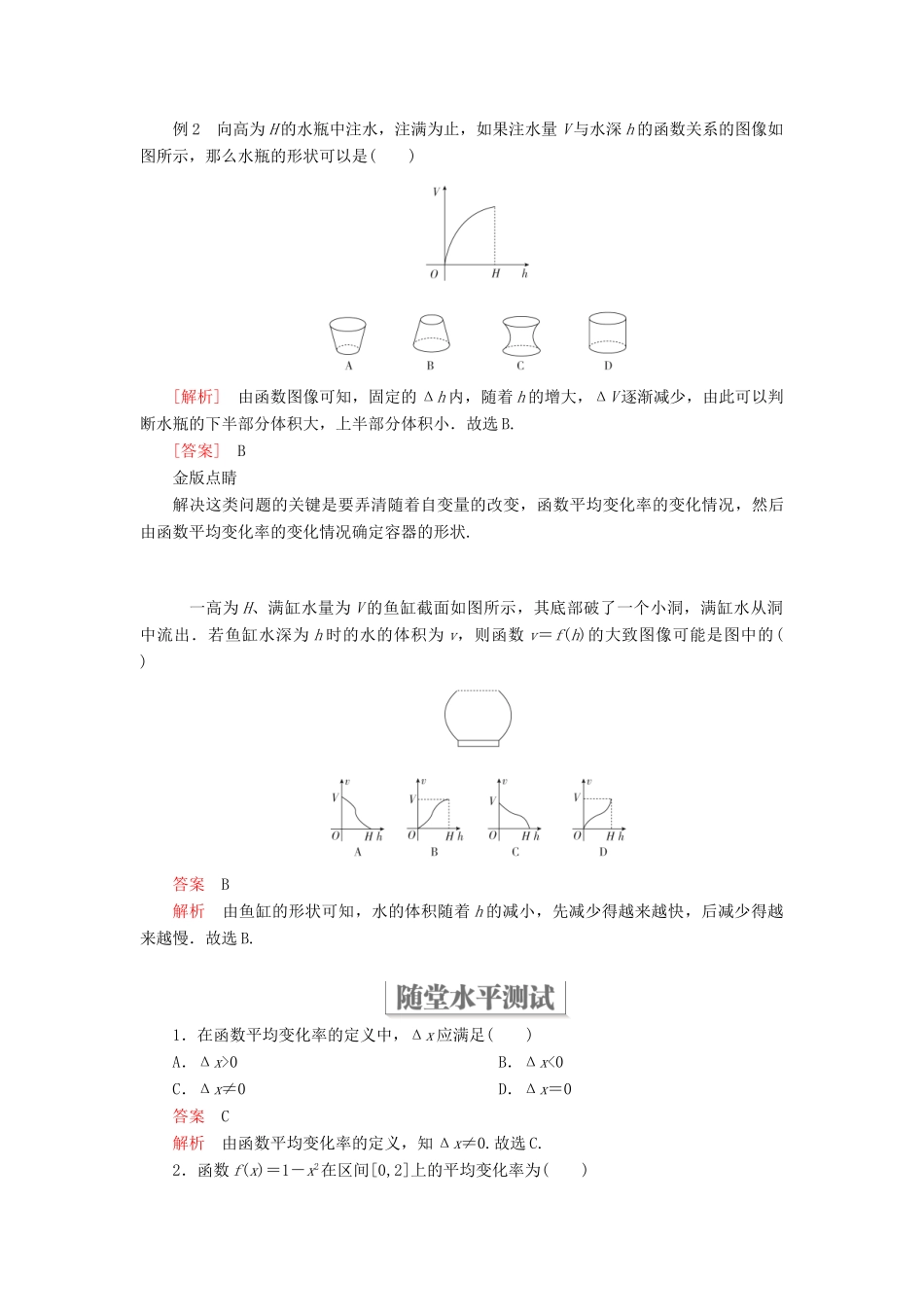
第 2 课时 函数的平均变化率(教师独具内容)课程标准:1.了解函数平均变化率的几何意义.2.理解函数递增和递减的充要条件,并能够运用函数递增和递减的充要条件判断函数的单调性.教学重点:函数递增和递减的充要条件.教学难点:运用函数递增和递减的充要条件证明函数的增减性.【情境导学】(教师独具内容)上节课我们学习了从函数单调性的定义来证明函数单调性的方法,那么证明函数的单调性还有没有其他方法呢?这节课我们就来研究证明函数单调性的另一种方法——函数的平均变化率.【知识导学】知识点一 函数平均变化率的定义一般地,对于函数 y=f(x),当 x1≠x2 时,称□=,为函数 y=f(x)在区间[x1,x2](x1x2时)上的平均变化率.知识点二 函数递增和递减的充要条件一般地,若 I 是函数 y=f(x)的定义域的子集,对任意 x1,x2∈I 且 x1≠x2,记 y1=f(x1),y2=f(x2),=,则:(1)y=f(x)在 I 上是增函数的充要条件是□>0 在 I 上恒成立;(2)y=f(x)在 I 上是减函数的充要条件是□<0 在 I 上恒成立.1.判一判(正确的打“√”,错误的打“×”)(1)对于给定平面直角坐标系中的任意两点 A(x1,y1),B(x2,y2),若记 Δx=x2-x1,Δy=y2-y1,则表示直线 AB 的斜率.( )(2)若函数 y=f(x)在(a,b)上是增函数,则在(a,b)上一定有>0.( )(3)在增函数和减函数的充要条件中,可以把“任意 x1,x2”改为“存在 x1,x2”.( )答案 (1)× (2)√ (3)×2.做一做(请把正确的答案写在横线上)(1)函数递增的充要条件是其图像上任意两点连线的斜率都________0,函数递减的充要条件是其图像上任意两点连线的斜率都________0.(2)函数:① f(x)=x2,② f(x)=,③ f(x)=|x|,④ f(x)=2x+1 中,满足对任意x1,x2∈(0,+∞),都有<0 的是________.(3)函数 f(x)=-x2-2x 的最大值是________.答案 (1)> < (2)② (3)1题型一 函数单调性的证明及应用例 1 证明:函数 f(x)=(x>0)在(0,1]上是增函数,在[1,+∞)上是减函数,并求这个函数的最值.[证明] 设 x1≠x2,则===.当 x1,x2∈(0,1]时,有 1-x1x2>0,从而>0,因此 f(x)在(0,1]上是增函数.当 x1,x2∈[1,+∞)时有 1-x1x2<0,从而<0,因此 f(x)在[1,+∞)上是减函数.由函数的单调性可知,函数没有最小值;而且,当 x∈(0,1]时,有 f(x)≤f(1),当 x∈[1,+∞)时,不等式 f(x)≤f(1)也成立.因此 f(1)...