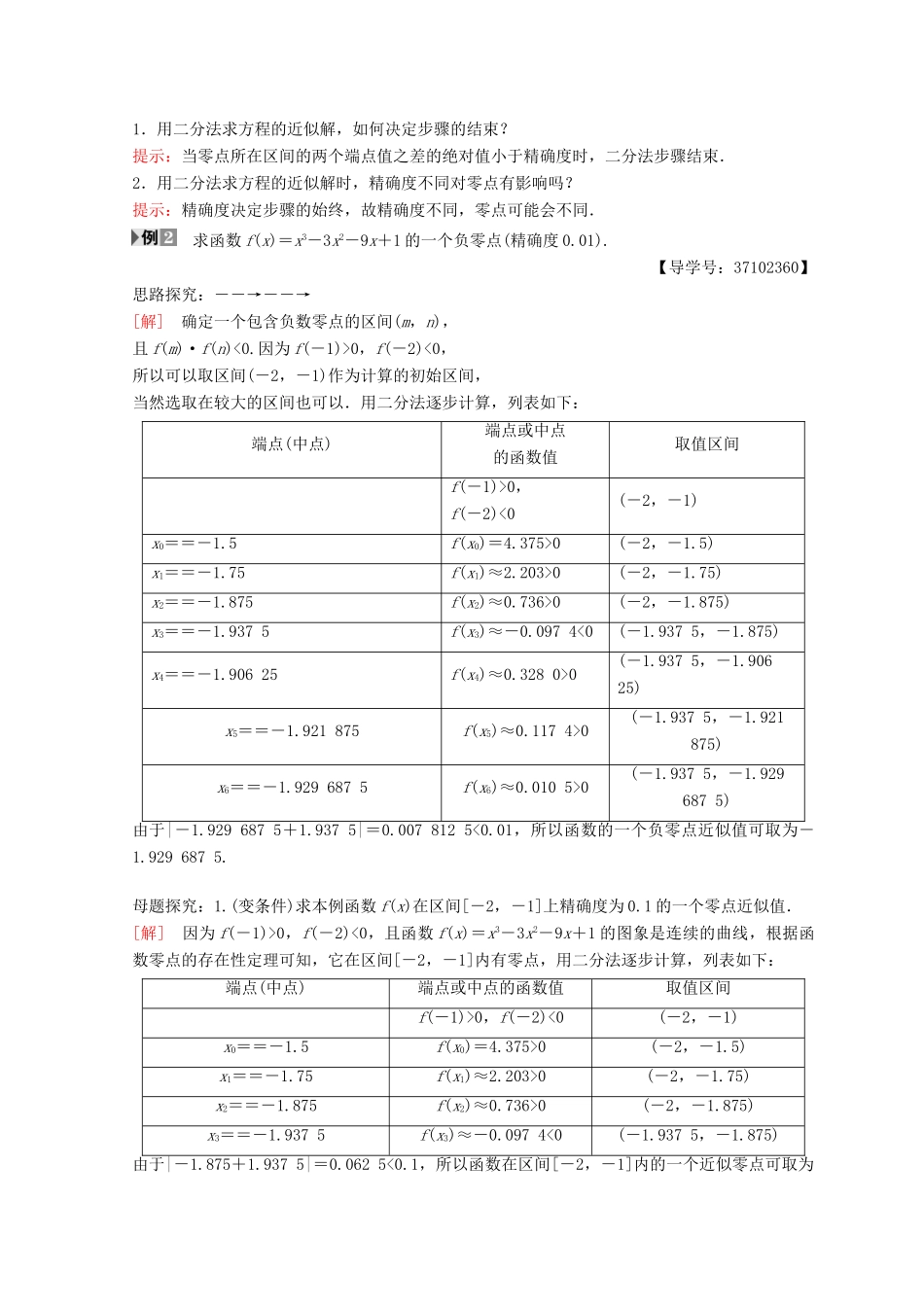
3.1.2 用二分法求方程的近似解学习目标:1.通过具体实例理解二分法的概念及其使用条件.(重点)2.了解二分法是求方程近似解的常用方法,能借助计算器用二分法求方程的近似解.(难点)3.会用二分法求一个函数在给定区间内的零点,从而求得方程的近似解.(易混点)[自 主 预 习·探 新 知]1.二分法的定义对于在区间[a,b]上连续不断且 f ( a )· f ( b )<0 的函数 y=f(x),通过不断地把函数 f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.思考:若函数 y=f(x)在定义域内有零点,该零点是否一定能用二分法求解?[提示] 二分法只适用于函数的变号零点(即函数在零点两侧符号相反),因此函数在零点两侧同号的零点不能用二分法求解,如 f(x)=(x-1)2的零点就不能用二分法求解.2.二分法求函数零点近似值的步骤[基础自测]1.思考辨析(1)二分法所求出的方程的解都是近似解.( )(2)函数 f(x)=|x|可以用二分法求零点.( )(3)用二分法求函数零点的近似值时,每次等分区间后,零点必定在右侧区间内.( )[答案] (1)× (2)× (3)×2.用二分法求函数 f(x)在(a,b)内的唯一零点时,精确度为 0.001,则结束计算的条件是( )A.|a-b|<0.1B.|a-b|<0.001C.|a-b|>0.001 D.|a-b|=0.001B [据二分法的步骤知当区间长度|b-a|小于精确度 ε 时,便可结束计算.]3.已知函数 y=f(x)的图象如图 311 所示,则不能利用二分法求解的零点是________.图 311x3 [ x3左右两侧的函数值同号,故其不能用二分法求解.]4.用二分法研究函数 f(x)=x3+3x-1 的零点时,第一次经过计算得 f(0)<0,f(0.5)>0,可得其中一个零点 x0∈________,第二次应计算________. 【导学号:37102358】(0,0.5) f(0.25) [ f(0)<0,f(0.5)>0,∴x0∈(0,0.5),故第二次应计算 f(0.25).][合 作 探 究·攻 重 难]二分法的概念 已知函数 f(x)的图象如图 312 所示,其中零点的个数与可以用二分法求解的个数分别为( )图 312A.4,4 B.3,4C.5,4 D.4,3D [图象与 x 轴有 4 个交点,所以零点的个数为 4;左右函数值异号的零点有 3 个,所以用二分法求解的个数为 3,故选 D.][规律方法] 判断一个函数能否用二分法求其零点的依据是:其图象在零点附近是连续不断的,且该零点为变号零点因此,用二分法求函数的零点近似值的方法仅对函数的变号零点适合,对函数的不变号...